Question

Два непропорциональных кубических многочлена с целыми коэффициентами имеют общий иррациональный корень. Докажите, что у них есть еще один общий корень

Answer 1

Поскольку, любое уравнение можно поделить на его старший коэффициент, то будем считать, для удобства, что мы рассматриваем два приведенных кубических уравнения с рациональными коэффициентами.

$x^3+ax^2+bx+c = 0\\x^3+mx^2+nx+k=0$, $a,b,c,m,n,k$ - рациональные числа.

Поскольку, данные уравнения имеют общий корень, то уравнение, являющееся их разностью, тоже содержит этот корень:

$(m-a)x^2+(n-b)x+(k-c) = 0$ , поскольку коэффициенты уравнений непропорциональны, то все коэффициенты полученного квадратного уравнения ненулевые.

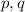А значит, данный общий иррациональный корень принимает вид : $p+-\sqrt{q}$ , где $p,q$ - рациональные числа, при этом 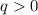$q0$ не полный квадрат, отсюда в частности $q\neq 0$.

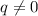Попробуем показать, что если  $p+\sqrt{q}$ корень уравнения

$x^3+ax^2+bx+c = 0$ , то и $p-\sqrt{q}$ корень данного уравнения , и наоборот. Сделаем некоторое упрощение.

Если число  $p+-\sqrt{q}$  является корнем данного уравнения , то сделаем замену:  $x-p=t$ , тогда после раскрытия скобок данное уравнение так же будет с рациональными коэффициентами и будет иметь корень  $t=+-\sqrt{q}$  

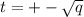
Такое уравнение примет вид :

$f(t)=t^3+ut^2+vt+g=0$ , $u,v,g$ - рациональные числа.

Учитывая, что $f(\sqrt{q} ) = 0$

$q\sqrt{q} +uq+v\sqrt{q} +g=0\\\sqrt{q} (q+v) = -g-uq$

Предположим, что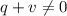 $q+v\neq 0$ , но тогда , учитывая, что 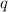$q$ - не полный квадрат, то левая часть равенства иррациональна, а правая  рациональна, что невозможно. То есть мы пришли к противоречию, а значит : $q+v=g+uq=0$

Таким образом:

$f(-\sqrt{q} ) =-q\sqrt{q} +uq -v\sqrt{q}+g = g+uq -\sqrt{q}(q+v) = 0$

Аналогично, доказывается, что если $-\sqrt[]{q}$ корень данного уравнения, то и $\sqrt{q}$ корень этого уравнения.

Таким образом, мы доказали, что если  $p+\sqrt{q}$ корень уравнения

$x^3+ax^2+bx+c = 0$ , то и $p-\sqrt{q}$ корень данного уравнения и наоборот.  Аналогично доказывается этот факт и для уравнения:

$x^3+mx^2+nx+k=0$ .

А значит, данные кубические многочлены имеют еще один общий иррациональный корень.

Что и требовалось доказать.