Рассмотрим последние цифры степеней чисел 3 и 7 (очевидно, степени чисел 33 и 77 оканчиваются на те же цифры; в таблице последняя цифра числа x обозначена как x mod 10):
Дальше таблицу можно не продолжать: поскольку последняя цифра степени определяется только последней цифрой предыдущей степени, то дальше всё будет повторяться: например, для степеней тройки дальше идут 3, 9, 7, 1, 3, 9, ... Таким образом, последовательность последних цифр степеней тройки и семёрки является периодической с периодом 4, то есть прибавление любого количества четвёрок к показателю степени последнюю цифру не меняет.
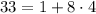, поэтому 
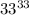оканчивается на ту же цифру, что и 
, то есть на 3. 
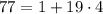, поэтому 
оканчивается на ту же цифру, что и 
, то есть на 7. Значит, сумма 
оканчивается на ту же цифру, что и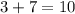 
, то есть на 0. Искомый остаток равен нулю.
ответ. 0
Объяснение:
В основе метода математической индукции (ММИ) лежит принцип математической индукции: утверждение $P(n)$ (где $n$ - натуральное число) справедливо при $\forall n \in N$, если:
Утверждение $P(n)$ справедливо при $n=1$.
Для $\forall k \in N$ из справедливости $P(k)$ следует справедливость $P(k+1)$.
Доказательство с метода математической индукции проводится в два этапа:
База индукции (базис индукции). Проверяется истинность утверждения при $n=1$ (или любом другом подходящем значении $n$)
Индуктивный переход (шаг индукции). Считая, что справедливо утверждение $P(k)$ при $n=k$, проверяется истинность утверждения $P(k+1)$ при $n=k+1$.
Метод математической индукции применяется в разных типах задач:
Доказательство делимости и кратности
Доказательство равенств и тождеств
Задачи с последовательностями
Доказательство неравенств
Нахождение суммы и произведения
второе действие: умножение члены с одинаковыми основаниями, путём сложения показателей степени