
Объяснение:
Часть 1
1. Параллелограммом называется четырехугольник, у которого противолежащие стороны ...
1.параллельны
2.равны
3.пересекаются
4.перпендикулярны
2. Дайте название следующему утверждению: в параллелограмме противоположные стороны равны. 1.определение параллелограмма
2.признак параллелограмма
3.аксиома
4.свойство параллелограмма
3)В параллелограмме ABCD углу А противоположным будет угол ?
1. В
2. С
3. D
4. В параллелограмме нет противоположных углов
4. Какова сумма любых двух соседних углов в параллелограмме?
1) 180°
2) бывает разной
3) 270°
4) 90°
5. В четырехугольнике два противоположных угла равны. Является ли он параллелограммом?
1) не является
2) не обязательно
3) такая ситуация невозможна
4) является
6. Один из углов параллелограмма равен 35°. Чему равны остальные его углы?
1) 145°, 35°, 145°;
2) 55°, 125°, 5°;
3) 35°, 145°, 50.
Сумма двух соседних углов равна 180°, значит второй угол : 180 - 35= 145°. Противоположные углы в параллелограмме равны , значит оставшиеся углы : 145°;35°; 145°
7. Биссектрисы соседних углов параллелограмма:
1) перпендикулярны
2) параллельны
3) пересекаются и точкой пересечения делятся пополам
4) невозможно их провести
8. Продолжите: Биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник.
9. Вставьте пропущенное слово: В параллелограмме противоположные стороны равны
10.Вставьте пропущенные слова: Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм
Часть 2 (задачи)
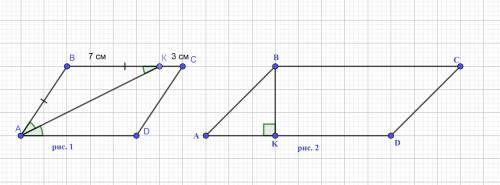
1.В параллелограмме АВСD биссектриса угла А пересекает сторону ВС в точке К так, что ВК = 7 см, КС = 3 см. Чему равен периметр параллелограмма?
Биссектриса угла в параллелограмме отсекает от него
равнобедренный треугольник, поэтому Δ АВК равнобедренный, значит АВ=ВК= 7 см
Сторона ВС=ВК+ КС= 7+3=10 см
Р=2*(АВ+ВС) =2*(10+7)=2*17 =34 см
ответ : Р= 34 см
( рис. 1 во вложении)
2. Из вершины В параллелограмма ABCD с острым углом А проведен перпендикуляр BK к прямой AD; ВК =1/2АВ. Найдите углы С и D
Рассмотрим Δ ABK. ( рис. 2) Он прямоугольный (∠ ВКА = 90°).
По условию BK = 1/ AB. А поскольку AB – гипотенуза Δ АВК ., то ∠ А = 30 ° (катет, лежащий против угла в 30 ° равен половине гипотенузы).
Поскольку в параллелограмме противолежащие углы равны, то
∠ С = 30 °
Теперь найдем ∠ D. В параллелограмме сумма внутренних углов равна 360 ° , значит
∠ D = ∠B = (360° - 2*30°):2= 150°.
ответ: C = 30 градусов, D = 150 градусов
( рис.2 во вложении)
Записать первые три члена ряда
Это уже, кстати, «боевое» задание – на практике довольно часто требуется записать несколько членов ряда.
Сначала , тогда:
Затем , тогда:
Потом , тогда:
Процесс можно продолжить до бесконечности, но по условию требовалось написать первые три члена ряда, поэтому записываем ответ:
Обратите внимание на принципиальное отличие от числовой последовательности,
в которой члены не суммируются, а рассматриваются как таковые.
Пример 2
Записать первые три члена ряда
Это пример для самостоятельного решения, ответ в конце урока
Даже для сложного на первый взгляд ряда не составляет трудности расписать его в развернутом виде:
Пример 3
Записать первые три члена ряда
На самом деле задание выполняется устно: мысленно подставляем в общий член ряда сначала , потом и . В итоге:
ответ оставляем в таком виде, полученные члены ряда лучше не упрощать, то есть не выполнять действия: , , . Почему? ответ в виде гораздо проще и удобнее проверять преподавателю.
Иногда встречается обратное задание
Пример 4
Записать сумму в свёрнутом виде с общим членом ряда
Здесь нет какого-то четкого алгоритма решения, закономерность нужно увидеть.
В данном случае:
Для проверки полученный ряд можно «расписать обратно» в развернутом виде.
А вот пример чуть сложнее для самостоятельного решения:
Пример 5
Записать сумму в свёрнутом виде с общим членом ряда
Выполнить проверку, снова записав ряд в развернутом виде
Объяснение:sdg
1. Полуплоскость
2. Треугольник
3. Угол
4. Луч