Общий вид квадратного уравнения:
ax² + bx + c = 0
через D₁).
3x² + 22x - 16 = 0
a = 3, b = 22, c = - 16,
k = b/2 =
= 22/2 = 11
D₁ = k² - ac = 11² - 3 · ( -16 )
= 121 + 48 = 169 = 13²
x₁,₂ = ( -k ± √D₁)/a = ( -11 ± √13² )/3 =
= ( -11 ± 13 )/3
x₁ = ( -11 - 13 )/3 = - 24/3 = -8
x₂ = ( -11 + 13 )/3 = 2/3
через D).
3x² + 22x - 16 = 0
a = 3, b = 22 , c = - 16
D = b² - 4ac = 22² - 4 · 3 · ( -16 ) =
= 484 + 192 = 676 = 26²
x₁,₂ = ( -b ± √D )/2a = ( -22 ± √26² )/2 · 3 =
= ( -22 ± 26 )/6
x₁ = ( -22 - 26 )/6 = - 48/6 = -8
x₂ = ( -22 + 26)/6 = 4/6 = 2/3
ответ: -8; 2/3.
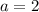
Объяснение:
Так, сначала восстановим меньшие коэффициенты 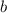 и
и  , а затем займёмся старшим коэффициентом
, а затем займёмся старшим коэффициентом  .
.
Начнём с коэффициента  . Как мы видим при
. Как мы видим при 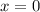 ,
, 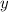 принимает значение
принимает значение  . Это значит, что свободный член (коэффициент
. Это значит, что свободный член (коэффициент  ) равен
) равен  .
.
Однако, есть ещё одна интересная деталь. При 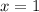 ,
, 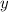 также принимает значение
также принимает значение  . Если мы подставим в уравнение
. Если мы подставим в уравнение 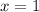 , то получим вот что:
, то получим вот что:
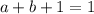 . Это означает, что коэффициенты
. Это означает, что коэффициенты  и
и 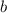 равны по значению, но противоположны по знаку. Иными словами:
равны по значению, но противоположны по знаку. Иными словами: 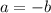 .
.
Координаты вершины параболы судя по графику 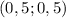 . И если с координатой абсцисс мы уже разобрались в наших логических рассуждениях, то нахождение координаты ординат нам выйти на коэффициенты
. И если с координатой абсцисс мы уже разобрались в наших логических рассуждениях, то нахождение координаты ординат нам выйти на коэффициенты  и
и 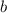 .
.
Так как  по числовой характеристике равно
по числовой характеристике равно 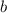 , то мы можем вместо
, то мы можем вместо 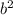 использовать
использовать 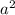 (так как отрицательное число в квадрате будет положительное число).
(так как отрицательное число в квадрате будет положительное число).
Координата ординаты вершины параболы вычисляется по формуле:
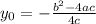
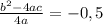
Найдём наконец коэффициент 
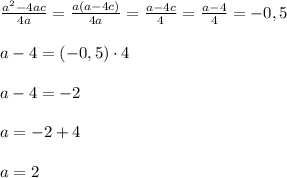
Теперь мы кстати можем восстановить функцию полностью:
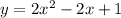
х1=-4-2✓7;х2=-4+2✓7
Объяснение:
х=-8+✓64+48/2
х=-8+✓112/2
х=-8+4✓7/2
х=-4+2✓7
х=-4-2✓7