Объяснение:
y=5ˣ.
Это показательная функция.
График этой функции показан на рис. 1.
Показательная функция y=5ˣ является строго монотонно возрастающей.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у∈(0;+∞).
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
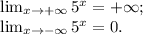
у=0,3ˣ
Это показательная функция.
График этой функции показан на рис. 2.
Показательная функция у=0,3ˣ является строго монотонно убывающей.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у∈(0;+∞).
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
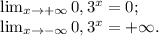
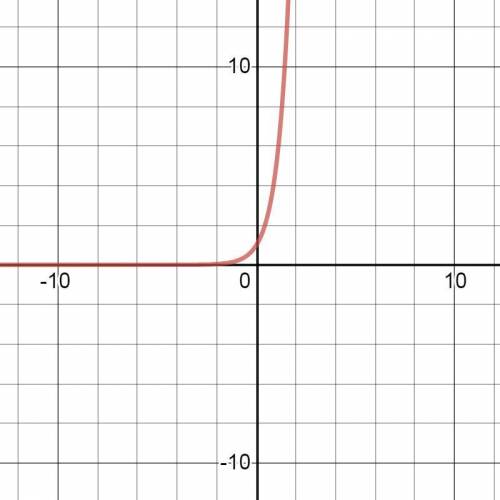
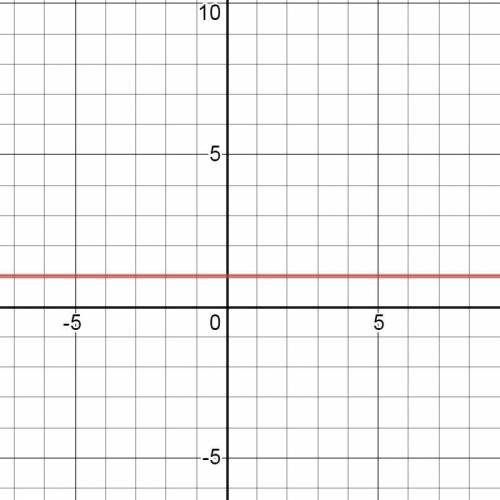
у=1ˣ.
График этой функции показан на рис. 3.
Единица в любой степени равена единице. ⇒
Получаем функцию у=1.
Графиком этой функции является график функции у=0 (ось ОХ),
смещённый вверх по оси ОУ на одну единицу.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у=1.
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
нужно рассматривать две разных ситуации:
1) x>=0
тогда y = 2x - 1/2 x^2 - x = - 1/2 x^2 + x
парабола, ветви вниз, корни 0 и 2
т.е. справа от оси У рисуем только часть этой параболы (от х=0)
2) x < 0
тогда у = 2*(-х) - 1/2 x^2 - (-x) = -2x -1/2 x^2 + x = -1/2 x^2 - x
парабола, ветви вниз, корни 0 и -2
т.е. слева от оси У рисуем только часть этой параболы (до х=0)
(получится похоже на то, как птицу-чайку рисуют ---два крыла...)
а вот про прямую у = kx ---точка (0; 0) принадлежит графику... и прямой с любым k...
т.е. общая точка будет всегда (т.е. нет таких k...)
Есть приложение в плей маркете там все напишишь и готово
Объяснение: