Question

Задача Фаульхабера. Докажите, что для любого натурального N верно рааенство​

Answer 1

Объяснение:

Мы докажем это равенство по индукции. Но сначала преобразуем правую часть равенства к более удобному для нас виду:

$\frac{1}{12} (2n^6+6n^5+5n^4-n^2)=\frac{n^2(2n^4+6n^3+5n^2-1)}{12} =\frac{n^2(2n^4+2n^3+4n^3+4n^2+n^2+n-n-1)}{12} =\frac{n^2(2n^3(n+1)+4n^2(n+1)+n(n+1)-(n+1))}{12} =\frac{n^2(n+1)(2n^3+4n^2+n-1)}{12} =\\=\frac{n^2(n+1)(2n^3+2n^2+2n^2+2n-n-1)}{12} =\frac{n^2(n+1)(2n^2(n+1)+2n(n+1)-(n+1))}{12}=\frac{n^2(n+1)^2(2n^2+2n-1)}{12}$А вот теперь применим индукцию. Легко проверить, что для n=1 равенство верно.

Теперь предположим что равенство верно для n=k:

$1^5+2^5+...+k^5=\frac{k^2(k+1)^2(2k^2+2k-1)}{12}$

Прибавив к обеим частям равенства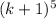 $(k+1)^5$ получим:

$1^5+2^5+...+k^5+(k+1)^5=\frac{k^2(k+1)^2(2k^2+2k-1)}{12}+(k+1)^5$

Займёмся преобразованием правой части этого равенства:

$\frac{k^2(k+1)^2(2k^2+2k-1)}{12}+(k+1)^5=(k+1)^2\bigg(\frac{k^2(2k^2+2k-1)}{12} +(k+1)^3\bigg)=\\=\frac{(k+1)^2}{12} \big(k^2(2k^2+2k-1)+12(k^3+3k^2+3k+1)\big)=\\=\frac{(k+1)^2}{12}\big(2k^4+14k^3+35k^2+36k+12\big)=\frac{(k+1)^2(2k^4+4k^3+10k^3+20k^2+15k^2+30k+6k+12)}{12}=\\=\frac{(k+1)^2(2k^3(k+2)+10k^2(k+2)+15k(k+2)+6(k+2))}{12}=\frac{(k+1)^2(k+2)(2k^3+10k^2+15k+6)}{12}=\\=\frac{(k+1)^2(k+2)(2k^3+4k^2+6k^2+12k+3k+6)}{12}=\frac{(k+1)^2(k+2)(2k^2(k+2)+6k(k+2)+3(k+2))}{12}=$$=\frac{(k+1)^2(k+2)^2(2k^2+6k+3)}{12}=\frac{(k+1)^2(k+2)^2(2(k+1)^2+2k+1)}{12}=\frac{(k+1)^2(k+2)^2(2(k+1)^2+2(k+1)-1)}{12}$Таким образом

$1^5+2^5+...+k^5+(k+1)^5=\frac{(k+1)^2(k+2)^2(2(k+1)^2+2(k+1)-1)}{12}$

То есть если равенство верно для произвольного n=k, то оно также оказывается верным и для n=k+1. По индукции заключаем верность равенства для любого натурального n.

Если же вас интересует каким можно вывести формулу, которую мы только что доказали - напишите мне в ЛС.