Докажите, что многочлен, тождественно равный выражению (x - 4)^2n + (x - 3)^n - 1, где n является натуральным, делится нацело га многочлен x^2 - 7x + 12
Добрый день! Я буду играть роль школьного учителя и с радостью помогу вам разобраться с данным вопросом.
Прежде чем перейти к решению, давайте разберемся, что представляет собой данная последовательность.
Последовательность – это набор чисел, который следует определенным правилам. В данном случае, у нас есть некая последовательность, где каждый элемент обозначается как аn, где n – это номер элемента в последовательности (например, a1, a2, a3 и так далее).
Теперь важно понять, что значит "а3(k+2)" и "а3(k+6)".
Выражение "а3(k+2)" означает, что мы берем элемент последовательности с номером 3 и прибавляем к нему число 2. Аналогично, выражение "а3(k+6)" означает, что мы берем элемент последовательности с номером 3 и прибавляем к нему число 6.
Таким образом, мы получаем два конкретных элемента последовательности: а3(k+2) и а3(k+6).
Для определения количества членов последовательности, расположенных между элементами а3(k+2) и а3(k+6), нам необходимо знать некоторые важные детали:
1) Как расположены элементы последовательности перед и после а3(k+2) и а3(k+6)?
Например, если последовательность выглядит следующим образом: а1, а2, а3, а4, а5... , то элемент а3 находится после а2 и перед а4. Подобным образом, а4 находится после а3 и перед а5.
2) Число k - это переменная, которая определяет, насколько элементов нужно сдвинуться внутри последовательности. Например, если k=1, то слово "k" будет заменено на 1, т.е. а3(1+2) превратится в а3(3) и т.д.
Теперь, когда у нас есть все необходимые сведения, можно приступить к решению задачи.
Допустим, у нас есть последовательность а1, а2, а3, а4, а5 и так далее.
Далее, нам нужно определить, сколько элементов расположено между а3(k+2) и а3(k+6).
Для этого нам нужно просто посчитать количество элементов между а3(k+2) и а3(k+6), не включая сами эти элементы в подсчет.
Давайте рассмотрим пример:
Предположим, у нас есть последовательность а1=2, а2=5, а3=9, а4=11, а5=13, а6=15, а7=17, а8=19, а9=21, а10=23 и так далее.
И пусть нам дано выражение: а3(k+2) и а3(k+6).
Если, например, мы возьмем k=2, то мы получим а3(2+2) и а3(2+6).
а3(2+2) превратится в а3(4), что равно 11.
а3(2+6) превратится в а3(8), что равно 19.
Таким образом, нам нужно определить, сколько элементов находится между 11 и 19.
Определить это можно путем подсчета элементов, не включая сами числа 11 и 19.
В нашем примере, элементы, расположенные между 11 и 19, составляют: 13, 15 и 17.
Значит, всего у нас 3 элемента, расположенных между а3(k+2) и а3(k+6).
Важно отметить, что окончательный ответ может меняться в зависимости от значения переменной k и самой последовательности. Поэтому, чтобы получить точный ответ, необходимо знать значения элементов последовательности и значение k.
Надеюсь, моё объяснение помогло вам понять, как определить количество членов последовательности, расположенных между а3(k+2) и а3(k+6). Если вам нужна дополнительная помощь или у вас возникнут дополнительные вопросы, пожалуйста, не стесняйтесь задавать их!
Ч.т.д.
_____________________
В решении использована Теорема Безу: остаток от деления многочлена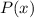
на двучлен 
равен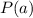 
.