-—--——---¯&------------------
1) (x+5)(x+2) > 0;
Для начала обозначим на координатной прямой нули ф-ции f(x) = (x+5)(x+2)
x + 5 = 0, x = -5
x + 2 = 0, x = -2
(смотри рисунок)
Точки исключенны так как строго >.
Найдем знак этой ф-ции на каждом из промежутков:
(-∞; -5) - берем например -10. Подставим в наше неравенство. Имеем:
(-10 + 5)(-10 + 2) = (-5) * (-8),
Тоесть там и там отрицательное но когда умножим дасть положительное число, тоесть 40.
Значит на прмежутке (-∞; -5) знак положительной.
(-5; -2) - аналогично. Берем например -3.Подставим:
(-3 + 5)(-3 + 2) = 2 * (-1) = -2 - отрицательное. Значит на промежутке (-5; -2) знак отрицательной.
(-2; +∞). Берем например 0:
(0 + 5)(0 + 2) = 5 * 2 = 10
Значит на промежутке (-2; +∞) знак положительный.
Поскольку У нас неравенство > то берем промежутки с положительным знаком.
ответ: (-∞; -5) U (-2; +∞)
2) (x+1)(x-4) ≤ 0;
Найдем нули ф-ции:
х + 1 =0, х = -1
х - 4 = 0, х = 4
Точки включены (зарисованые)
на промежутке (-∞; -1] - положительный знак
на пр-ке [-1; 4] - отрицательный
на пр-ке [4; +∞) - положительной.
Поскольке ≤, то ответ: [-1; 4]
3)
точку 7 - включить, а точку -8 - исключить
Смотри рисунок.
(-∞; -8) - "+"
(-8; 7] - "-"
[7; +∞) - "+"
ответ: (-8; 7]
4)
Точка -6 - включить; точку 10 - исключить
(∞; -6] - "+"
[-6;10) - "-"
(10; +∞) - "+"
ответ: (∞; -6] U (10; +∞)
5) (x-1) x (x+3)> 0;
x = 1
x = 0
x = -3
Все точки исключены.
(-∞; -3) - "-"
(-3; 0) - "+"
(0; 1) - "-"
(1; +∞) - "+"
ответ: (-3; 0) U (1; +∞)
6) x(x+2)(x-3) > 0
x = 0
x = -2
x = 3
Все точки исключены.
(-∞; -2) - "-"
(-2; 0) - "+"
(0; 3) - "-"
(3; +∞) - "+"
ответ: (-2; 0) U (3; +∞)
7)
Все точки исключены.
(-∞; -1) - "-"
(-1; 0) - "+"
(0; 0,5) - "-"
(0,5; +∞) - "+"
ответ: (-1; 0) U (0,5; +∞)
8)
Точки 0 и -1/3 - включать, а точку 2 - нет.
(-∞; -1/3] - "-"
[-1/3; 0] - "+"
[0; 2) - "-"
(2; +∞) - "+"
ответ: (-∞; -1/3] U [0; 2)
1) 6см. 9 см. 30 см.
2) 15 км/час.
Объяснение:
Площадь прямоугольника, одна из сторон которого на 3 см больше другой, равна 54 см2.
Найдите стороны и периметр прямоугольника.
Решение.
Пусть одна сторона равна х см. Тогда другая равна х+3 см.
Площадь S=ab или S=x*(x+3);
x²+3x-54=0;
x1=6; x2= -9 - не соответствует условию.
х=6 см = величина одной из сторон.
х+3=6+3=9 см = величина второй стороны.
Периметр прямоугольника равен Р=2(a+b)=2 (6+9)=2*15=30 см.
***
2. Катер 5 км по течению
и 8 км по озеру,
затратив на весь путь 1 ч.
Скорость течения реки равна 3 км/ч.
Найдите скорость катера по течению.
Решение.
пусть х км/час - скорость катера в стоячей воде (по озеру).
Тогда по течению реки скорость будет равна х+3 км/час.
На путь 8 км по озеру катер затратил 8/х часов.
На путь 5 км по течению катер затратил 5/(х+3) часа.
На весь путь затратил 1 час.
8/х+5/(х+3)=1;
8(х+3)+5х=х(х+3);
8х+24+5х=х²+3х;
х²+3х-8х-5х-24=0;
х²-10х-24=0;
По теореме Виета
х1+х2=10; х1*х2=-24;
х1=12; x2= -2 - не соответствует условию
х=12 км/час - скорость катера в стоячей воде.
х+3= 12+3=15 км/час - скорость катера по течению.
1
Объяснение:
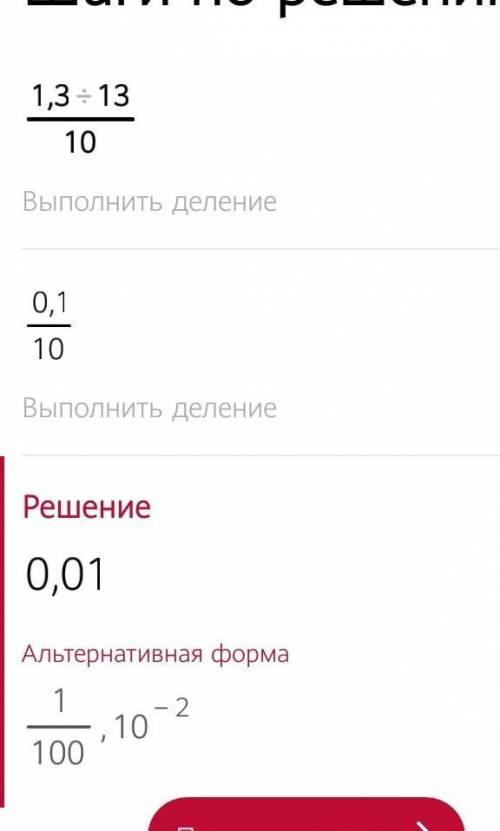
13/10=1.3
1.3/1.3=1