a)=а*4b=4ab(числа нужно сокращать)
в) m2-n2 можно разложить на (m-n)*(n+m), а в 3m-9n можно 3 вынести за скобки, получиться 3(m-3n). Сделая это получим m-3n/m+n * (m-n)*(m+n)/3(m-3n). Дальше сокращаем и получаем 1/1 * m-n/3. Одинки шлём нахер и получаемm-n/3
б) деление заменяем умножением, получаем 21x3y2 * 3:7x3y2. После сокращения получаем 3 * 3/у. Умножаем и остаётся 9/у
г) Разлаживаем x2-16 на (x+4)*(x-4), а у x2-4x можем х вынести за скобки. Получим x(x-4). Можем сразу деление заменить умножением (x-4)*(x+4)/(x+2)2 * x+2/x(x-4). После сокращения получаем x+4/x+2 * 1/x=x+4/x(x+2)
Для того чтобы геометрическая прогрессия была бесконечно убывающей, знаменатель геометрической прогрессии 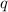 должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.
должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.
Графически это выглядит так: 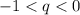 или
или 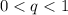 .
.
Рассмотрим наши примеры:
1) 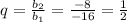 . Выполняются ли условия неравенства?
. Выполняются ли условия неравенства?
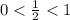 . Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
2) 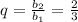 . Выполняются ли условия неравенства?
. Выполняются ли условия неравенства?
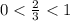 . Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
3) 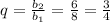 . Выполняются ли условия неравенства?
. Выполняются ли условия неравенства?
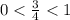 . Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.