Пусть x км/ч — скорость второго автомобиля, тогда (x + 10) км/ч — скорость первого автомобиля. Они встретились через 3 часа. За это время второй автомобиль проехал 3x км, а первый автомобиль — 3(x + 10) км. Используя эти данные и условия задачи, составим уравнение и решим его:
3(x + 10) + 3x = 450,
3x + 30 + 3x = 450,
6x = 450 - 30,
6x = 420,
x = 420 / 6,
x = 70 км/ч.
Мы нашли скорость второго автомобиля. Теперь найдем скорость второго автомобиля:
70 + 10 = 80 км/ч.
ответ: скорость первого автомобиля равна 80 км/ч, скорость второго автомобиля — 70 км/ч.
Объяснение:
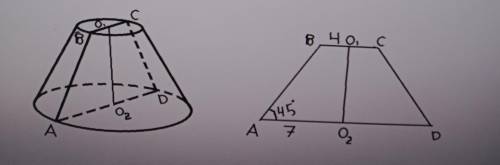
V=(1/3) π h(r₁²+r₁*r₂+r₂²), гда r₁=r=4 r₂=R=7
h=О₁О₂=7-4=3/см/
т.к. ∠АВD=45°, если из вершины В опустить перпендикуляр ВВ₂ на АО₂, то АВ₂=ВВ₂= ОО₂=3 см.
V=(1/3) π 3(4²+4*7*+7²)=π(16+28+49)=93π