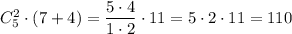
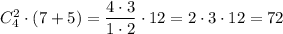
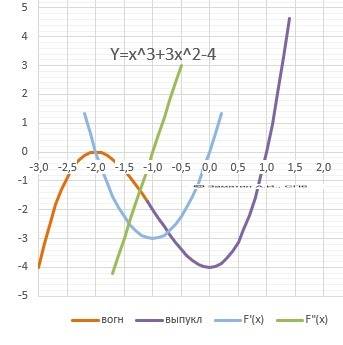
1. Область определения - Х∈(-∞;+∞) - непрерывная.
Вертикальных асимптот - нет
2. Пересечение с осью Х. Y=0
При х1 = x2 = - 2, x3 = 1
3. Пересечение с осью У. У(0) = -4
4. Поведение на бесконечности.
limY(-∞) = - ∞ и limY(+∞) = +∞
Горизонтальной асимптоты - нет
5. Исследование на чётность.
Y(-x) ≠ - Y(x)
Функция ни чётная ни нечетная - общего вида..
6. Производная функции.
Y'(x)= 3*x² + 6*x = 3*x*(x+2) = 0
7. Корень при Х= - 2.
Возрастает - Х∈(-∞;-2)∪(0;+∞)
максимум - Y(-2) =0
минимум - Y(0) = - 4
Убывает - X∈(-2;0)
8. Вторая производная
Y"(x) = 6*x +6 = 6*(x+1)
9. Точка перегиба
Y"(x)=0 при X=-1
Выпуклая - Х∈(-∞;-1] Вогнутая - Х∈[-1;+∞).
10. График в приложении.
пусть x(м) это ширина бассейна, тогда длина бассейна- (x+6) м. Расстояние между бассейном и дорожкой 0.5м.Длина дорожки- x+0.5+0.5=(x+1), а ширина (x+6+1)=(x+7)
Sдорожки= (x+1)(x+7)м.кв
Sбассейна= x(x+6) м.кв
а по условию задачи Sдорожки- 15м.кв
Составим уравнение:
(x+1)(x+7)-x(x+6)=15
x^2+7x+x+7-x^2-6x=15
7x+x-6x=15-7
2x=8 /:2
x=4 (м)- ширина бассейна
2) 4+6=10 (м)- длина бассейна
ответ: 4м, 10м