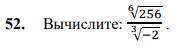
![\frac{ \sqrt[6]{256} }{ \sqrt[3]{ - 2} } = \frac{2 \sqrt[6]{ {2}^{2} } }{ - \sqrt[3]{2} } = \frac{2 \sqrt[3]{2} }{ - \sqrt[3]{2} } = - 2](/tpl/images/1419/8660/654cf.png)
• Решение:
— Чтобы узнать, возрастает или убывает функция y=6-3x, нужно использовать вот такие правила:
• 1. Смотрим на то, что стоит перед функцией ( знак «+» или «-» ) .
• 2. Мы увидели, какой знак стоит перед функцией. Это знак «-». Теперь, переходим к следующему пункту нашего правила.
• 3. Теперь, чтобы нам легче узнать, возрастающая или убывающая эта функция, возьмём пример с возрастающей функцией и убывающей. Например: y=6x-2. В данном случае функция возрастающая, т.к. перед «x» подразумевается знак «+». А вот возьмём ещё один пример, только с убывающей функцией: -x+1. Перед «х» стоит знак «-», значит, функция убывающая
• 4. Ну, а теперь, по примеру, будем определять: возрастает или убывает функция y=6-3x .
• 5. y=6-3x. Мы видим, то что перед «х» стоит знак «-», значит, функция убывающая.
• ответ:
Функция y=6-3x убывает.
— Фу-у-ух, как же я это долго писала! Надеюсь, я Вам и остальным участникам! Удачи! :³