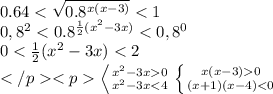
(-1;0) (3;4)
В решении.
Объяснение:
Задание 1.
Известно, что график функции f(x) проходит через точку (−5; 3) и параллелен графику функции y = −4x + 3.
а) Найдите уравнение данной функции f(x) ( ).
Графики линейных функций параллельны, если k₁ = k₂, а b₁ ≠ b₂.
k₁ = -4, значит, k₂ = -4;
Вычислить b₂:
Подставить в уравнение известные значения х и у (координаты точки) и вычислить b₂:
3 = -4 * (- 5) + b₂:
3 = 20 + b₂:
3 - 20 = b₂:
b₂ = -17;
Уравнение второй функции:
у = -4х - 17.
б) Постройте график данной функции f(x) ( ).
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
y = −4x + 3 у = -4х - 17
Таблицы:
х -1 0 1 х -6 -5 -4
у 7 3 -1 у 7 3 -1
По вычисленным точкам построить графики.
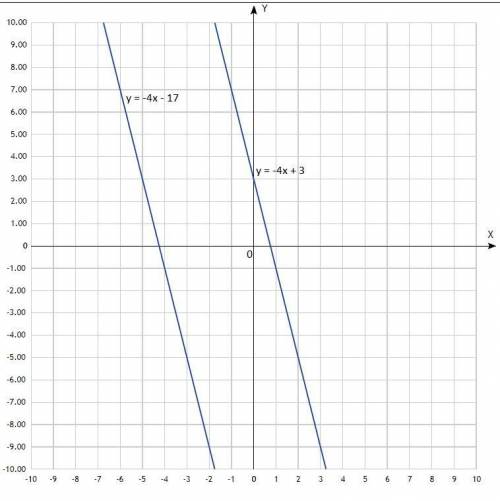
0.64 = 0.8^2
корень(0.8^(x(x-3))) = 0.8^(x(x-3)/2)
1 = любое число, не равное 0, в степени 0
0.8 < 1 --- функция убывающая, т.е. бОльшему значению аргумента соответствует меньшее значение функции, поэтому
2 > x(x-3)/2 > 0
0 < x(x-3) < 4
x(x-3) > 0 x(x-3) < 4
x > 0 ___ x > 3 ___ x(x-3) < 4
x > 3 ___ x^2 -3x -4 < 0
x > 3 ___ (x + 1)(x - 4) < 0 по т.Виета x1 = -1 x2 = 4
x > 3 ___ x + 1 < 0 ___ x - 4 > 0
x > 3 ___ x < -1 ___ x > 4 нет решения
или
x > 3 ___ x + 1 > 0 ___ x - 4 < 0
x > 3 ___ x > -1 ___ x < 4 3 < x < 4
или
x < 0 ___ x < 3 ___ x(x-3) < 4
x < 0 ___ (x + 1)(x - 4) < 0
x < 0 ___ x < -1 ___ x > 4 нет решения
или
x < 0 ___ x > -1 ___ x < 4 -1 < x < 0