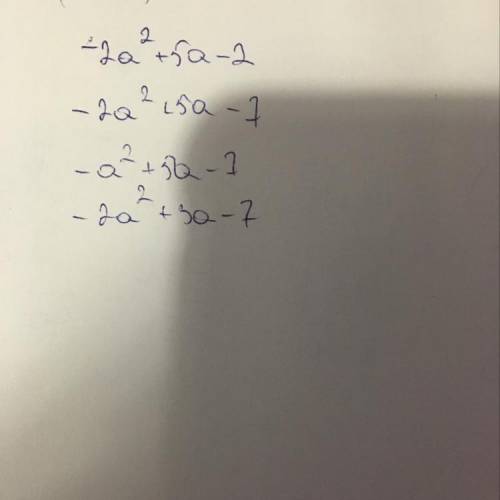
1). R = 12 см
l = 2πR·α / 360°
1. l = 2π·12·36° / 360° = 24π/10 = 2,4π см
2. l = 2π·12·72° / 360° = 4,8π см
3. l = 2π·12·45° / 360° = 3π см
4. l = 2π·12·15° / 360° = π см
2) l = 2πR R = l / (2π)
S = πR² = πl² / (4π²) = l² / (4π)
1. l = 6π см
S = 36π² / (4π) = 9π см
2. l = 4π см
S = 16π² / (4π) = 4π см²
3. l = 10π см
S = 100π² / (4π) = 25π см²
4. l = 8π см
S = 64π² / (4π) = 16π см²
3)
а) R = 12 см,
l = πR·α / 180°
α = l · 180° / (πR)
1. l = 2π см
α = 2π · 180° / (12π) = 30°
2. l = 3π см
α = 3π · 180° / (12π) = 45°
б) R = 10 см,
Sсект = πR²·α / 360°
α = Sсект·360° / (πR²)
1. Sсект = 5π см²
α = 5π·360° / (100π) = 18°
2. Sсект = 10π см²
α = 10π·360° / (100π) = 36°
В решении.
Объяснение:
Формула движения: S=v*t
S - расстояние v - скорость t – время
Дано:
S = 280 км
17 км/час - собственная скорость теплохода.
40 часов (всего времени) - 6 часов (стоянка) = 34 часа (в пути).
х - скорость течения реки.
280/(17+х) - время теплохода по течению.
280/(17-х) - время теплохода против течения.
По условию задачи уравнение:
280/(17+х) + 280/(17-х) = 34
Умножить все части уравнения на (17-х)(17+х), чтобы избавиться от дробного выражения.
280 * (17-х) + 280 * (17+х) = 34 * (17-х)(17+х)
4760 - 280х + 4760 + 280х = 9826 - 34х²
9520 = 9826 - 34х²
34х² = 9826 - 9520
34х² = 306
х² = 9
х = √9
х = 3 (км/час) - скорость течения реки.
Проверка:
280/20 + 280/14 = 14 + 20 = 34 (часа), верно.