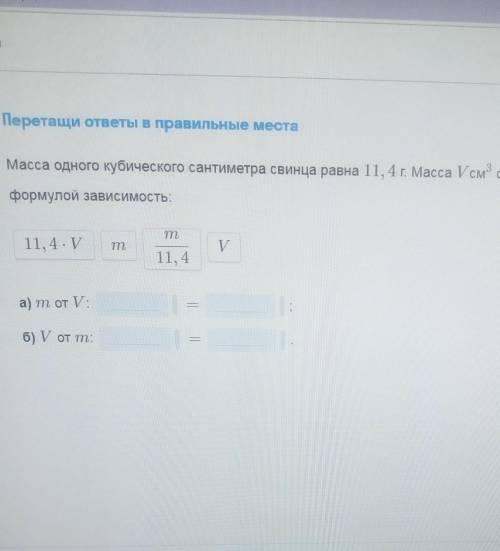
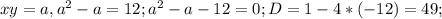
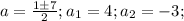, вот теперь мы можем заменить первое уравнение на более простое и решить 2 системы, объединив их решения.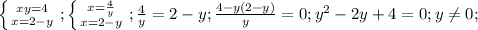 
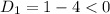, корней нет. Решаем вторую систему: 
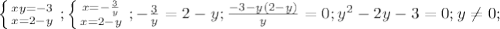Здесь b=a+c (-2=1-3), тогда 
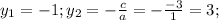, а теперь в любое уравнение подставляем каждое из получившихся и в ответе пишем 2 точки: 
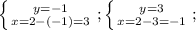, получили точки (3;-1);(-1;3). Довольно похожие значения, объясняется это всё квадратами в первом уравнении системы. ответ:(3;-1);(-1;3).
Для решения запишем формулу бинома Ньютона:
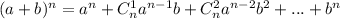
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение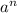 
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение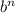 
.
Рассмотрим многочлен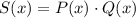 
, где:
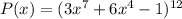
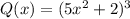
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена :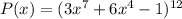
- степень определяется выражением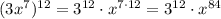 
, то есть степень равна 84
- свободный член равен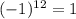 
Для многочлена :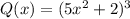
- степень определяется выражением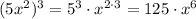 
, то есть степень равна 6
- свободный член равен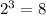 
Наконец, для многочлена 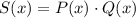получим:
- степень определяется выражением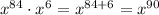 
, то есть степень равна 90
- свободный член равен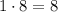 
Сумма степени и свободного члена многочлена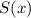 
:
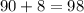
ответ: 98
:ииттььь