

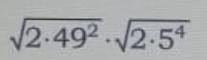







Цель задачи найти наименьшее число, которое делится на 35.
Разложим число 35 = 5 * 7,
значит число 49*** должно одновременно делится и на 5 и на 7.
Рассуждаем.
1) Признак делимости числа 49*** на 5 это такое число, у которого последняя цифра делится на 5. Из чётных чисел наименьшее это - 0.
Предварительно число имеет вид 49**0.
2) Рассмотрим теперь признак делимости на 7.
По определению число делится на 7 если результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.
Т.к. последняя цифра 0, то достаточно рассмотреть только число 49**.
Запишем иначе: 49ХУ, тогда из определения
(49Х - 2*У) = - этот полученный результат доложен делится на 7.
Из выражения видно, что наименьшее чётная цифра, которая будет обеспечивать признак делимости на 7 это - 0 , т.е. число 4900
тогда
490 - 2 * 0 = 490 - это число делится на 7.
Получаем наименьшее число 49000 - которое делится на 35, но по условию задачи цифры должны быть различные.
Тогда ближайшие числа которые должны делится на 7 это:
4922; 4924; 4926 и 4928
Проверим делимость на 7
492 - 2*2 = 488 ⇒ 48 - 2 * 8 = 32 не делится на 7
492 - 2*4 = 484 ⇒ 48 - 2 * 4 = 40 не делится на 7
492 - 2*6 = 480 ⇒ 48 - 2 * 0 = 48 не делится на 7
492 - 2*8 = 476 ⇒ 47 - 2 * 6 = 35 делится на 7
Окончательно запишем 49280 наименьшее число с различными цифрами, которое делится на 35
ответ: 49280 - наименьшее число которое делится на 35.
Так как последняя цифра четна и число кратно 5 , то она равна нулю , а само число кратно 70 , запишем его в виде : A = 49000 +100x +10y , где x и y - число сотен и десятков числа А , х≠0 , так как двух нулей быть не должно , 49000 кратно 70 ⇒ 100х+10y также кратно 70 ( оно равно А -49000) и должно быть наименьшим , рассмотрим трехзначные числа, кратные 70 -140 , 210 , 280 , 350 и т .д., наименьшее число из этой последовательности с различными четными цифрами равно 280 ⇒ А =49280
ответ :49280