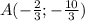
Наименьшее значение 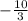
Объяснение:
x + 2y - 1 = 0 ⇔ 2y = 1 - x ⇔ 
Введем функцию 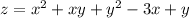 и найдем её частные производные:
и найдем её частные производные:
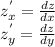
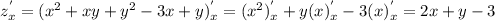
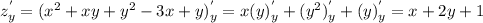
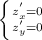
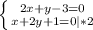
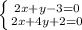
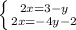 ⇒ 3 - y = -4y - 2
⇒ 3 - y = -4y - 2
3 - y = -4y - 2
3y = -5|:3
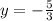
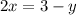 ⇒
⇒ 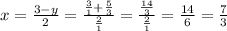
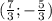
Пусть координаты точки 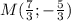
Минимум функции достигается при 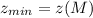
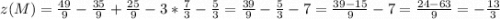
Проверим принадлежит ли точка M прямой 
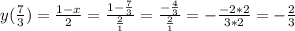
Точка 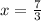 не принадлежит прямой
не принадлежит прямой  так как
так как 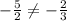
x + 2y - 1 = 0 ⇒ x = 1 - 2y
Введем функцию 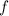 при этом x выразим через y так данная точка лежит на прямой x + 2y - 1 = 0 и на графике функции
при этом x выразим через y так данная точка лежит на прямой x + 2y - 1 = 0 и на графике функции 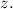
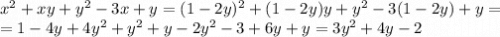
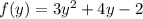
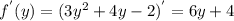
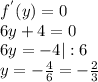
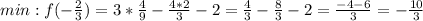
Точка минимума функции  которая принадлежит графику x + 2y - 1 = 0 это точка A с координатами
которая принадлежит графику x + 2y - 1 = 0 это точка A с координатами 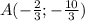
Наименьшее значение 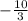
а) sin a * cos a * tg a.
Применим основное тригонометрическое тождество tg a = (sin a)/(cos a), и заменим tg a на (sin a)/(cos a).
sin a * cos a * (sin a)/(cos a).
Сократим cos a и cos a.
sin a * sin a = sin²a.
б) sin a * cos a * ctg a - 1.
По формуле ctg a = (cos a)/(sin a) заменим в данном выражении ctg a.
sin a * cos a * (cos a)/(sin a) - 1.
Сократим sin a и sin a.
cos a * cos a - 1 = cos²a - 1.
Заменим 1 на (sin²a + cos²a), т.к. sin²a + cos²a = 1.
cos²a - (sin²a + cos²a) = cos²a - sin²a - cos²a = -sin²a.
в) sin²a - tg a * ctg a.
Заменим tg a * ctg a на 1, т.к. tg a * ctg a = 1.
sin²a - 1.
Заменим 1 на (sin²a + cos²a).
sin²a - (sin²a + cos²a) = sin²a - sin²a - cos²a = -cos²a.
г) tg a * ctg a + ctg²a.
Заменим (tg a * ctg a) на 1.
1 + ctg²a = 1/sin²a.
Объяснение:
все что я нашел