
Данное уравнение не имеет целых корней.
Используем метод Феррари:
уравнение вида
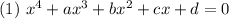
с замены 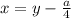
приводим к виду:
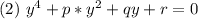
где:
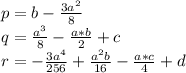
добавим и вычтем из левой части уравнения 2 выражение 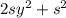 , где s - некоторое число:
, где s - некоторое число:

получим:
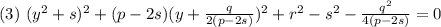
Пусть s - корень уравнения
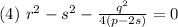
Тогда уравнение 3 примет вид:
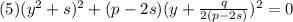
Избавляемся в уравнении 4 от знаменателя:
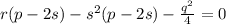
Раскроем скобки и получим:
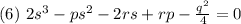
Уравнение 6 называется кубической резольвентой уравнения 4 степени.
Разложим уравнение 5 на множители:
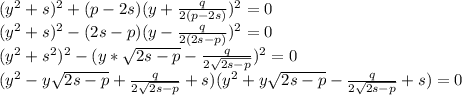
Получим два квадратных уравнения:
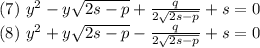
Применяем этот метод для решения уравнения
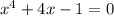
Перепишем уравнение в полном виде:
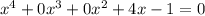
коэффиценты:
a=0
b=0
c=4
d=-1
определяем p,q и r:
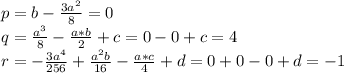
ищем s:
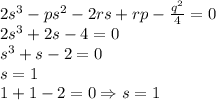
подставляем p,q,r и s в квадратные уравнения 7 и 8:
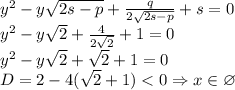
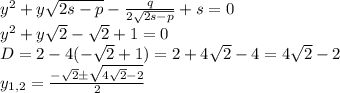
Теперь находим x:
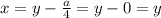
ответ: 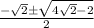
Так как первый велосипедист проезжает за 3 ч на 18 км больше,чем второй за 2 ч. , то 3x- 2y=18
Так как расстояние между городами равно 52 км и велосипедисты встретились через 2 ч после начала движения, то 2(x+y)=52
Получили систему уравнений:3x-2y=18 и 2(x+y)=52
2(x+y)=52
x+y=26
x=26-y
Подставляем значение х в уравнение 3x-2y=18
3(26-y)-2y=18
78-3y-2y=18
-5y=-60
y=12(км/ч)-скорость второго
x=26-y
x=26-12
x=14(км/ч)-скорость первого велосипедиста.