В решении.
Объяснение:
Постройте график функции x + y= -1 и 3x + 3y = -2.
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразовать уравнения в уравнения функций.
x + y= -1 3x + 3y = -2
у = -1 - х 3у = -2 - 3х
у = (-2 - 3х)/3
у = -х -2/3
Таблицы:
х -1 0 1 х -1 0 1
у 0 -1 -2 у 1/3 -2/3 -1 и 2/3
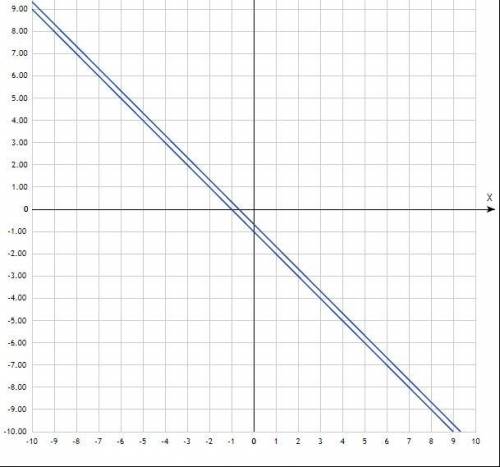
Судя по уравнениям функций, можно сразу сделать вывод, что графики данных функций параллельны: k₁ = k₂, b₁ ≠ b₂.
Всё решается очень просто. Применяется теорема Виета для первого уравнения (это есть в любом учебнике математики)
х(квадрат)+5х-7=0
х1*х2=-7
х1+х2=-5
Если надо составить уравнение с корнями 1/х1 и 1/х2, то надо сделать несколько преобразований:
Если х1*х2=-7, то применяя теорему Виета уже для второго уравнения, получаем, что (1/х1)*(1/х2)=-1/7
Тоже самое если сложить два корня:
(1/х1)+(1/х2)=(х1+х2)/(х1*х2)=-5/(-7)=5/7
Значит уравнение вот такое a^2-(5/7)a-(1/7)=0
Можно последнее уравнение умножить на 7, чтобы были целые коэффиценты.
Вот и всё решение.
решение на фотографии