x² + (m - 1)x + m² - 1,5 = 0
По теореме Виета :
x₁ + x₂ = - (m - 1)
x₁ * x₂ = m² - 1,5
x₁² + x₂² = (x₁ + x₂)² - 2x₁ * x₂ = (- (m - 1))² - 2 * (m² - 1,5) = m² - 2m + 1 - 2m² + 3 = - m² - 2m + 4
Найдём производную полученного выражения :
(- m² - 2m + 4)'= -2m - 2
Приравняем к нулю и найдём нули производной :
- 2m - 2 = 0
m + 1 = 0
m = - 1
Отметим полученное число на числовой прямой и найдём знаки производной на промежутках, на которые разбивается числовая прямая :
+ -
- 1
↑ max ↓
ответ : при m = - 1 сумма корней уравнения наибольшая
В обеих точках функция непрерывна
Объяснение:
Для ответа на данный вопрос найдём пределы слева и справа от указанных точек, если пределы совпадают, то функция в данной точке непрерывна, если не совпадают, то функция имеет разрыв первого рода, а если хотя бы один из пределов равен бесконечности или не существует, то в данной точке функция имеет разрыв второго рода.
для x = 0
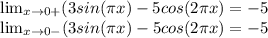
Как видим, пределы слева и справа совпадают, следовательно f(0) непрерывна
для x = 1
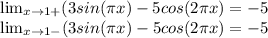
Снова видим, что пределы совпадают, следовательно и при f(1) функция непрерывна.
пусть х²=с
тогда:
с²-10с+9=0
по теореме Виета:
с1+с2=-(-10)=10
с1×с2=9
с1=1
с2=9
х²=с1
х²=1
х1=1
х2=-1
х²=с2
х²=9
х3=3
х4=-3
Проверка:
х⁴-10х²+9=0
(-1)⁴-10×(-1)²+9=0
1-10+9=0
0=0-истина.
1⁴-10×1²+9=0
1-10+9=0
0=0-истина.
(-3)⁴-10×(-3)²+9=0
81-90+9=0
0=0-истина.
3⁴-10×3²+9=0
81-90+9=0
0=0-истина.
ответ: х1=1; х2=-1; х3=3 и х4=-3.