Объяснение:
1 . ( x² - x )/3 = ( 2x + 4 )/5 ; │X 15 2 . ( 2x² + x )/5 = ( 4x - 2 )/3 ;│X 15
5( x² - x ) = 3( 2x + 4 ) ; 3( 2x² + x ) = 5( 4x - 2 ) ;
5x² - 5x = 6x + 12 ; 6x² + 3x = 20x - 10 ;
5x² - 5x - 6x - 12 = 0 ; 6x² + 3x - 20x + 10 = 0 ;
5x² - 11x - 12 = 0 ; 6x² - 17x + 10 = 0 ;
D = 361 > 0 ; x₁ = - 0,8 ; x₂ = 3 . D = 49 > 0 ; x₁ = 5/6 ; x₂ = 12/13 .
3 . ( x² - x )/2 = 5 + 6x ;│X 2
x² - x = 10 + 12x ;
x² - x - 12x - 10 = 0 ;
x² - 13x - 10 = 0 ; D = 209 > 0 ; x₁= (13 - √209 )/2 ; x₂ = (13 - √209 )/2 .


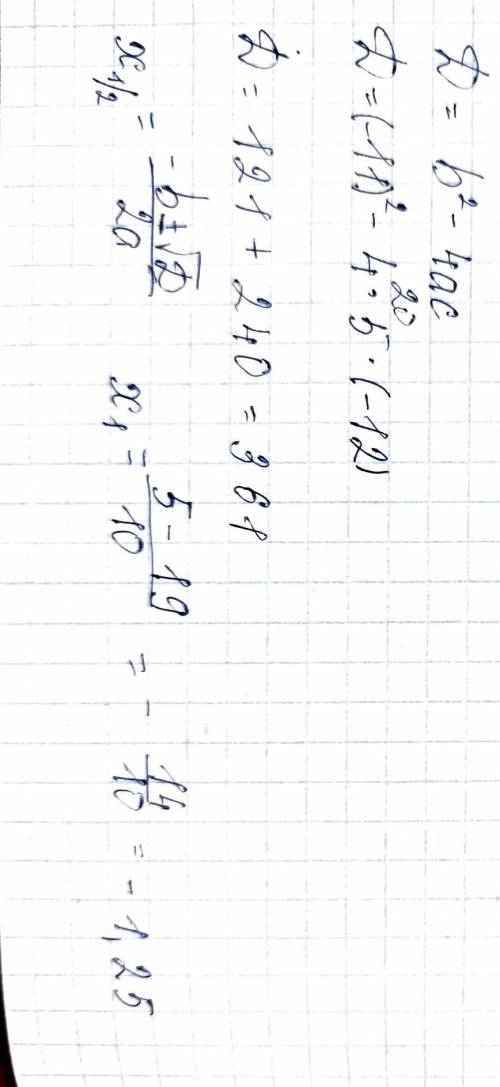
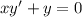
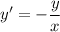 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными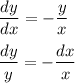
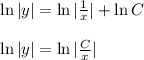
 - общее решение
- общее решение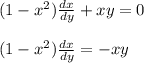

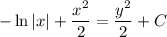 - общий интеграл
- общий интеграл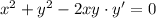

 , тогда
, тогда 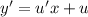



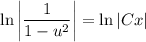
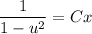
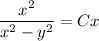 - общий интеграл
- общий интеграл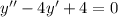
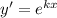 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
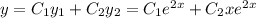 - общее решение
- общее решение
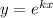 , тогда получаем
, тогда получаем
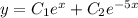

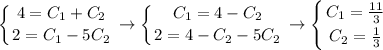
 - частное решение
- частное решение