(х² + 2х + 2)(х² + 2х - 4)= -5
Пусть t = х² + 2х + 2
(х² + 2х + 2)(х² + 2х + 2 - 6)= -5
t (t - 6) = -5
t² - 6t = -5
t² - 6t + 5 = 0
D = b² - 4ac = 36 - 4 · 1 · 5 = 16
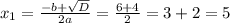
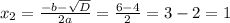
х² + 2х + 2 = 5
х² + 2х -3 = 0
D = b² - 4ac = 4 - 4 · 1 · (-3) = 16
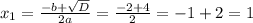
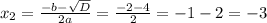
х² + 2х + 2 = 1
х² + 2х + 1 = 0
D = b² - 4ac = 4 - 4 · 1 · 1 = 0
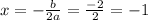
ответ: -3; -1; 1.
Пусть t = х² + 2х - 4
(х² + 2х - 4 + 6)(х² + 2х - 4) = -5
(t + 6)t = -5
t² - 6t = -5
t² - 6t + 5 = 0
D = b² - 4ac = 36 - 4 · 1 · 5 = 16
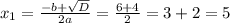
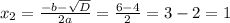
х² + 2х + 2 = 5
х² + 2х -3 = 0
D = b² - 4ac = 4 - 4 · 1 · (-3) = 16
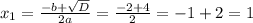
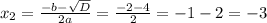
х² + 2х + 2 = 1
х² + 2х + 1 = 0
D = b² - 4ac = 4 - 4 · 1 · 1 = 0
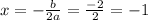
ответ: -3; -1; 1.
(см. объяснение)
Объяснение:
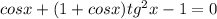 , ОДЗ:
, ОДЗ: 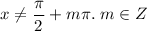
Попробуем решить это уравнение относительно тангенса:
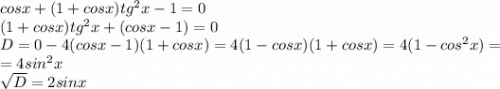
Тогда получили два случая:
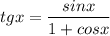 или
или 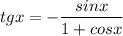
Применив формулу для тангенса половинного угла, получим:
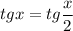 или
или 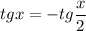
Применив формулы суммы и разности тангенсов и выполнив очевидные преобразования, получим:
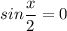 или
или 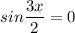
Решим каждое уравнение по отдельности:
1) 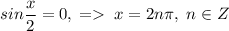
2) 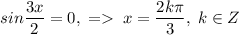
Окончательное решение уравнения с учетом ОДЗ:
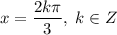
Найдем теперь корни уравнения, которые удовлетворяют неравенству 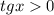 :
:
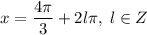
Задание выполнено!
Комментарий:
Замечу, что исходное уравнение можно упростить до вида:
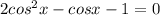
Откуда хорошо видно, что его корень:
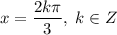
Такое решение также является допустимым.
ответ: вот , только что сделала
Объяснение: