Пусть второй бригаде понадобилось бы х дней на то, чтобы в одиночку сделать эту работу.
Тогда первой бригаде понадобилось бы x+10 дней.
Часть работы, которую за день выполняет вторая бригада в одиночку, выражается числом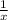 
.
Тогда часть работы, выполняемую в день первой, выразим так: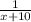 
.
Сначала, по условию, первая бригада работала 5 дней в одиночку, так что она успела сделать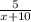 
всей работы.
Потом к ней подключилась вторая, и в течение 15 дней они выполнили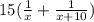 
всей работы.
Вся выполненная работа выражается следующим образом:
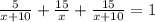
Далее,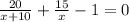 
Избавимся от знаменателя дроби и приведем подобные члены, тогда получим:
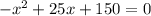
Получим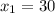 
, 
. Через x мы выражали количество дней, которое потребовалось бы второй бригаде на то, чтобы справиться в одиночку, а оно не может быть отрицательным. Значит, вторая бригада сделала бы эту работу за 30 дней, а первая - за 40.
1 + корень из (2х + 7) = х - 3.
возводим обе части в квадрат.
1 + 2 корня из (2х +7) + 2х + 7 = х2 - 6х + 9
2 корня из (2х +7) = х2 - 6х + 9 - 1 - 2х - 7
2 корня из (2х +7) = х2 - 8х + 1
возводим обе части в квадрат.
4 умножить на (2х + 7) = (х2 - 8х + 1)(х2 - 8х + 1)
8х + 14 = х4 - 8х3 + х2 + 64 х2 - 8х + х2 - 8х +1
х4 - 8х3 + 66 х2 - 24х - 13 = 0
Корни уравнений с высшими степенями находятся среди свободного члена.
-13 делится на 1; -1; 13; - 13
Дальше эти числа подставляешь в многочлен, и ищешь то число, при котором многочлен равен 0. Эти числа не подходят, значит уравнения корней не имеет (Я совершила где-то ошибку, проверь мои вычисления)