Нет точки максимума
Объяснение:
Рассмотрим функцию
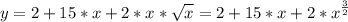
Так как в составе функции участвует квадратный корень, то область определений функции: x≥0, то есть D(y)=[0; +∞).
Чтобы найти экстремумы (локальные минимумы и максимумы) будем исследовать функцию с производной функции. Вычислим производную функции:
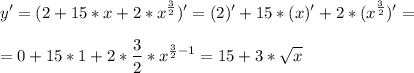
Так как 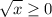 , то
, то
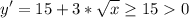
для любого x∈D(y). Это означает, что данная функция монотонно возрастает в D(y). Отсюда следует, что у функции нет точки максимума.
Так как функция монотонно возрастает в D(y), то минимальное значение в D(y)=[0; +∞) принимает при x=0: y(0)=2.
2)y^2(y-x)+1(y-x)=(y^2+1)(y-x)
1) m(m-1)-n(m-1)=(m-n)(m-1)=(17.2-7.2)(17.2--1)=10*16.2=162
2)x(2y-3)-y(2y-3)=(x-y)(2y-3)=(11.5-6.5)(2*6.5--3)=50