
ответ: а ∈ (1 ; 3)
Объяснение:
x² + (2a + 4)x + 8a + 1 ≤ 0
Левая часть выражения - квадратичная функция, графиком которой является парабола с ветвями, направленными вверх (коэффициент перед х² равен 1, положительный).
Неравенство не будет иметь решений, если парабола не будет пересекать ось Ох, т.е. квадратный трехчлен не будет иметь корней. А он не имеет корней, если дискриминант отрицательный.
Поэтому составим выражение для дискриминанта и решим неравенство D < 0.
D = (2a + 4)² - 4 · (8a + 1) = 4a² + 16a + 16 - 32a - 4 = 4a² - 16a + 12
4a² - 16a + 12 < 0
a² - 4a + 3 < 0
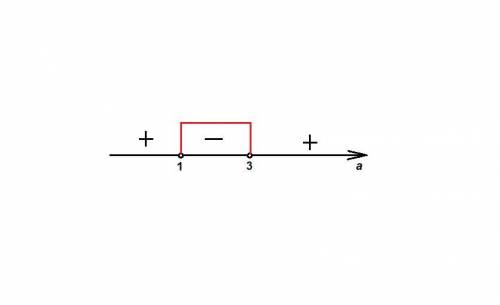
Решаем методом интервалов:
Найдем нули:
a² - 4a + 3 = 0
D/4 = 4 - 3 = 1
a₁ = 2 - 1 = 1
a₂ = 2 + 1 = 3
Отметим точки на координатной прямой (см. рисунок).
Решение неравенства а ∈ (1 ; 3).
Но попробуем распутаться
Пусть скорость первого пешехода х км в час.
Тогда он он км со скоростью х, потом стоял 1,5 часа, потом еще 12 км со скоростью (х+2) км в час
За это же время второй км. Скорость его у км в час
Составим уравнение
4/х + 1,5+ 12/(х+2)=18/у
Если бы. первый не делал остановки, то он пршел бы 4 км со скоростью х км в час, потом еще 13км со скорость х+2. Потому что они бы встретились посредине. Это значит первый бы 17 км и второй 17 км
4/х+13/(х+2)=17/у
ВЫразим 4/х +12/(х+2)=18/у-1,5
Подстави во второе
18/у -1,5 + 1/(х+2)=17/у
1/у +1/(х+2)=1,5, отсюда 1/у=1,5 -1/(х+2)
Подставим в преове уравнение
4/х+1,5+12/(х+2)= 18 ·(1,5-1/(х+2))
4/х +30/(х+2)=25,5
Решить это уравнение