рассмотрим сначала многочлен
5 ⋅ x 2 ⋅ y + 2 ⋅ y 3 − x ⋅ y + 1 5·x2·y+2·y3−x·y+1
: его члены имеют стандартный вид, подобные члены отсутствуют, значит многочлен задан в стандартном виде, и никаких дополнительных действий не требуется.
Теперь разберем многочлен
0 , 8 + 2 ⋅ a 3 ⋅ 0 , 6 − b ⋅ a ⋅ b 4 ⋅ b 5 0,8+2·a3·0,6−b·a·b4·b5
. В его состав входят нестандартные одночлены: 2 ⋅ a 3 ⋅ 0 , 6 и − b ⋅ a ⋅ b 4 ⋅ b 5 2·a3·0,6 и −b·a·b4·b5, т.е. имеем необходимость привести многочлен к стандартному виду, для чего первым действием преобразуем одночлены в стандартный вид: 2 ⋅ a 3 ⋅ 0 , 6 = 1 , 2 ⋅ a 3 2·a3·0,6=1,2·a3; − b ⋅ a ⋅ b 4 ⋅ b 5 = − a ⋅ b 1 + 4 + 5 = − a ⋅ b 10 −b·a·b4·b5=−a·b1+4+5=−a·b10, таким образом получаем следующий многочлен: 0 , 8 + 2 ⋅ a 3 ⋅ 0 , 6 − b ⋅ a ⋅ b 4 ⋅ b 5 = 0 , 8 + 1 , 2 ⋅ a 3 − a ⋅ b 10 0,8+2·a3·0,6−b·a·b4·b5=0,8+1,2·a3−a·b10. В полученном многочлене все члены – стандартные, подобных членов не имеется, значит наши действия по приведению многочлена к стандартному виду завершены.
1. пусть эти два числа будут a и b, тогда запишем систему
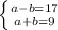
выявим а
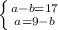
подставляем a в первое выражение и получается
9 - b - b = 17
9 - 2b = 17
-2b = 17-9
-2b = 8
b = -4
и теперь значение b подставляем во второе выражение, чтобы найти a
a = 9 - (-4)
a = 9 + 4
a = 13
ответ: числа 13 и -4
2. пусть эти два числа будут a и b, тогда запишем систему
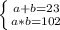
выявим a в первом выражении
a = 23-b
и теперь подставим это значение во второе выражение
(23-b)b = 102
23b-b^2 = 102
-b^2 + 23b -102 =0 --решаем квадратное уравнение через дискриминант
D = 529 -408= 121
1b =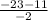 
= 17 a=23-17=6
2b = 
= 6 a=23-6=17
ответ: числа 17 и 6
3. пусть эти два числа будут a и b, тогда запишем систему
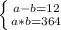
выявим a в первом выражении
a = 12+b
и теперь подставим это значение во второе выражение
(12+b)b=364
b^2 + 12b =364
b^2 +12b - 364 = 0 --решаем квадратное уравнение через дискриминант
D= 144 + 1456= 1600
1b =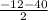 
= -26 a=12-26=-14
2b =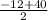 
= 14 a=12+14=26
ответ: числа -26 и -14; 14 и 26
скажите