a5=a1+4d
система
a8=a1+7d
a1+4d=8,7
система віднімемо від другого рівняння перше
a1+7d=12,3
a5=a1+4d
система
3d=3,6
d=1,2
система
a1=a5-4d
d=1,2
система
a1=3,9
Надеюсь, что решаю именно так, как это требуется)))
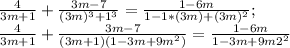
Итак, мы получили вот такое уравнение
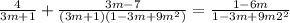
Видно, что приведением к общему знаменателю оно и решится
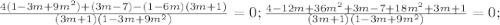
Приводим подобные
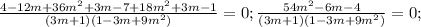
Числитель должен быть равен 0, при этом одновременно знаменатель не равен 0. Это равносильная система. Заметим сразу, что вторая скобка не равна нулю (неполный квадрат вообще всегда не равен 0), она не влияет на ограничения.
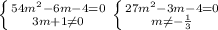
Решим квадратное уравнение.
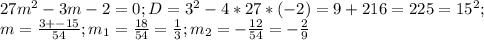
Как видно, ни одна треть, ни две девятые не соответствуют ограничению m≠-1/3, значит, оба значения идут в ответ.
ответ: 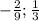
Теперь решим другое уравнение:
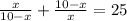
Сразу же возникают ограничения 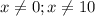
Теперь сделаем замену 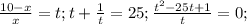
t=0 не является корнем этого уравнения, поэтому его даже не учитываем

Переходим к уравнениям
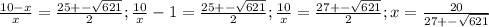
Получили вот такие интересности. Далее заметим, что 621 = 27*23, тогда вынесем 27 из под корня и преобразуем: 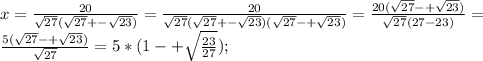
Теперь пишем ответ
ответ: 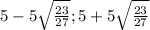
Примечание. "+-" - это знак "±", с "-+" аналогично (в редакторе формул его нет просто)
В 1-ом задании была важна формула суммы кубов
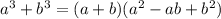
Во 2-ом задании следствие формулы разности квадратов 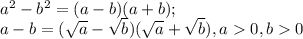
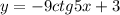
а5=8,7
а=8,7:5
а=1,74
1,74*5=8,7
а8=12,3
а=12,3:8
а=1,5375
1,5375*8=12,3