10х+2х-х+5=11х+5
Объяснение:
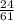проте ймовірність того, що листок містить саме число 2 менша та дорівнює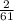 
Объяснение:
У високостном році 366, є місяці по 31 денів по 30 днів та у лютому 29 днів
Тож подивимось скількі днів у місяці містять двійку:
це номери 2, 12, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 - загалом це 12 днів на місяць,
як бачимо у кожному місяці високостного року по 12 днів із цифрою 2
тому на рік таких днів буде 12*12=144
а ймовірність такої події 
--------------------------
якщо ж казати про можливість натрапити саме на число 2 на листочку то це лише 
, оскыльки других днів у році стількиж скіль ки ж і місяців у році, а саме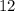 
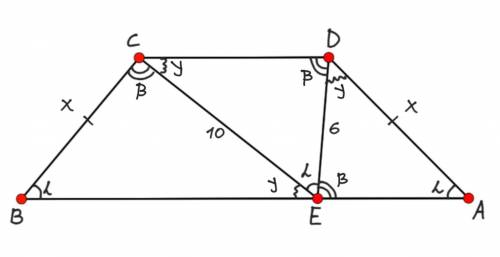
Дано: ABCD — трапеция, ВС=AD, АВ||CD, т.Е∈АВ;
∠СВА=∠DAE=∠DEC, DE=6, EC=10.
Найти: ВЕ:АЕ.
Решение.
∠СВА=∠DAE=∠DEC=α.
∠DEA=∠CDE=β как накрест лежащие при секущей ED и AB||CD.
∠BEC=∠ECD=γ как накрест лежащие при секущей ЕС и AB||CD.
Прямая АВ, т.Е лежит на ней. ∠ВЕС+∠CED+∠DEA=180°.
В ΔCBE: ∠CBA=α, ∠BEC=γ, ∠ВСЕ=β.
В ΔEDC: ∠DEC=α, ∠CDE=β, ∠ECD=γ.
В ΔEAD: ∠DAE=α, ∠DEA=β, ∠EDA=γ.
Треугольники СВЕ, EDC и EAD подобны (по трем углам)
Значит, их соответственные стороны относятся.
Пусть BC=AD=x.
Через подобные треугольники СВЕ и EAD найдем (выразим) стороны ВЕ и АЕ.
1) ВЕ/AD=CE/ED;
BE/x= 10/6;
BE= 10x/6;
BE= 5x/3.
2) BC/AE=CE/ED;
x/AE= 10/6;
AE= 6x/10;
AE= 3x/5.
BE:AE= 5x/3 : 3x/5 = 5x/3 • 5/3x= 25x/9x= 25:9.
ответ: ВЕ:АЕ=25:9.
Объяснение:
Фотомач