Так как в уравнении есть квадратные корни, то запишем ОДЗ:
Также заметим, что в левой части записано произведение двух неотрицательных выражений. Значит, правая часть уравнения также неотрицательна:
Таким образом, при уравнение не имеет корней.
Предположим, что . Тогда:
Проверим, удовлетворяют ли найденные корни ОДЗ.
Для первого корня получим:
Однако, квадратный корень не может принимать отрицательных значений. Значит, рассматриваемое выражение не является корнем уравнения ни при каких значениях параметра .
Для второго корня получим:
Последнее условие выполняется при любых значениях параметра . Но как отмечалось ранее, уравнение может иметь корни только при . Значит, данное выражение является корнем уравнения при .
Для любого неотрицательного выражения A: (при отрицательном А не имеет смысла) причем <=>
сумма двух неотрицательных выражений равняется 0, если каждое из выражений равно 0, значит данное уравнение равносильно системе уравнений которая очевидно не имеет корней (уравнения имеют разные корни) а значит и исходное уравнение не имеет корней ----------------------------------- иначе в левой части возрастающая функция как сумма двух возрастающих (функция корня и суперпозиция возрастающих функций корня и линейной) ОДЗ функции задающей левую часть а значит а значит данное уравнение не может иметь корней (левая часть заведомо больше правой) ------------- иначе подносим обе части к квадрату решений нет(проверка не нужна так как не нашли корней) ответ: данное уравнение корней не имеет
Так как в уравнении есть квадратные корни, то запишем ОДЗ:
Также заметим, что в левой части записано произведение двух неотрицательных выражений. Значит, правая часть уравнения также неотрицательна:
Таким образом, при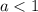 уравнение не имеет корней.
уравнение не имеет корней.
Предположим, что . Тогда:
. Тогда:
Проверим, удовлетворяют ли найденные корни ОДЗ.
Для первого корня получим:
Однако, квадратный корень не может принимать отрицательных значений. Значит, рассматриваемое выражение не является корнем уравнения ни при каких значениях параметра .
.
Для второго корня получим:
Последнее условие выполняется при любых значениях параметра . Но как отмечалось ранее, уравнение может иметь корни только при
. Но как отмечалось ранее, уравнение может иметь корни только при  . Значит, данное выражение является корнем уравнения при
. Значит, данное выражение является корнем уравнения при  .
.
при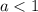 : нет корней,
: нет корней,
при :
: 