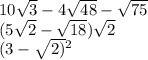
Відповідь:
66 или 68
Пояснення:
Пусть х - число монет в первом столбике, тогда х+1 - во втором, х+3 - в третьем, х+n- в n-столбце
Имеем арифметическую прогрессию с начальним значением=х, d=1. n+1 елементов, тогда можем записать сумму
(2х+n)/2 ×(n+1)=2021
х=2021/(n+1) -n/2
2021=43×47 розложение на простие делители, поетому столбиков может бить 43 или 47
Значит n может равняться 42 или 46
При n=42 по формуле имеем х=26. поетому количество монет в последнем максимальном столбике = х+n=68
При n=46. х=20 тогда монет будет 66
Решение.
1)
По теореме Виета
х₁ + х₂ = 3
По условию
4х₁+3х₂=15
2) Решаем полученную систему:
{х₁+х₂ = 3
{4х₁+3х₂ = 15
Умножим первое уравнение на (- 3)
{-3х₁ - 3х₂ = - 9
{4х₁ + 3х₂ = 15
Сложим
- 3х₁ - 3х₂ + 4х₁ + 3х₂ = - 9 + 15
х₁ = 6
Подставим в первое уравнение х₁ = 6 и найдем х₂
6 + х₂ =3
х ₂ = 3 - 6
х₂ = - 3
3) По теореме Виета
х₁ * х₂ = m
m = 6 * (-3)
m = - 18
ответ: х₁ = 6;
х₂ = - 3
m = - 18