
1) x² + 2x - 8 = (x - 2)(x + 4)
Для условия x² + 2 - 8:
x² + 2 - 8 = x² - 6 = (x - √6)(x + √6)
2) 3x₂ - 11x + 8 = (x - 1)(3x - 8)
Объяснение:
1) а) x² + 2x - 8
Найдем корни квадратного трехчлена по т.Виета: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
x₁ + x₂ = -2; x₁*x₂ = -8
⇒ корни данного квадратного трехчлена x₁ = -4; x₂ = 2
Разложим выражение на множители:
x² + 2x - 8 = (x - 2)(x + 4)
б) x² + 2 - 8
Упростим выражение и найдем его корни:
x² + 2 - 8 = x² - 6
x₁ = √6; x₂ = -√6
Тогда x² + 2 - 8 = x² - 6 = (x - √6)(x + √6)
2) 3x² - 11x + 8
Найдем корни квадратного трехчлена с дискриминанта:
D = b² - 4ac = 11² - 4*3*8 = 121 - 96 = 25 = 5²
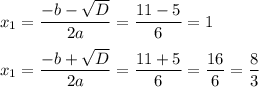
Разложим квадратный трехчлен на множители:
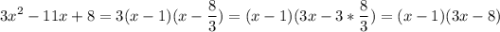
(Множитель 3 внесли во вторую скобку или вторую скобку умножили на 3).
20 км/ч и 30 км/ч
Объяснение:
Пусть время, за которое первый катер проходит 60 км равно t ч, тогда время, за которое второй катер проходит 60 км равно t-1 ч.
Значит, скорость первого катера равна 60/t км/ч, а время второго катера равно 60/(t-1) км/ч.
По условию задачи, катера двигались навстречу друг другу и за 1 час вместе 50 км. Составим уравнение:
(60/t + 60/(t-1))*1=50 |*t(t-1)
60(t-1)+60t=50t(t-1)
60t-60+60t=50t²-50t
50t²-170t+60=0 |:10
5t²-17t+6=0
D=(-17)²-4*5*6=289-120=169=13²
t₁=(17+13)/(2*5) = 30/10=3
t₂=(17-13)/(2*5)=4/10=0,4
Если t=3 ч, то t-1=3-1=2 ч
Если t=0,4 ч, то t-1=0,4-1=-0,6 <0 (невозможно, т.к. время не может быть отрицательным)
Следовательно, скорость первого катера равна 60/3=20 км/ч, а скорость второго катера равна 60/2=30 км/ч