![22262y63 \sqrt[33 \alpha \sec( \alpha \sec( \sin(\pi \infty \binom{ log_{ \\ \binom{\% ln( \alpha \csc( \sin( \sec( \tan( \sec( \csc( \beta \%\% log_{\pi \infty ln( \infty \sec( \sec(?) ) ) }(?) ) ) ) ) ) ) ) }{?} }(?) }{?} ) ) ) ]{?} ti \: lox \: y))( \sqrt{ \sqrt[ | \sqrt[.1 - + 788 = 0.. \geqslant \geqslant \leqslant < | | \sqrt[ \sqrt{ \frac{ { {xy)(789954330 = = + - \div \\ }^{2} }^{?} \times \frac{?}{?} }{?} } ]{?} | | ]{?} | ]{?} } \times \frac{?}{?}](/tpl/images/1608/4207/52c1a.png)
Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2) 
. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б) 
при 
Если x = -5, то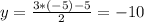 
Если х= 3, то 
Значит, 
Теплоход в движении был 13-3=10 часов.
Скорость теплохода по течению равна 20+4=24км/ч.
Скорость теплохода против течения равна 20-4=16 км/ч.
Пусть по течению теплоход шел х часов, а против течения - у часов. Зная, что всего в движении он был 10 часов, составляем первое уравнение:
х+у=10
По течению теплоход х км, против течения - 16у. Зная, что оба расстояния равны, составляем второе уравнение:
24х=16у.
Получили систему уравнений:
⇒
24(10-у) = 16у
24у + 16у = 240
у = 6
х = 10-6 = 4
Теплоход по течению плыл 4 часа, а это 24·4 = 96 (км)
За весь рейс теплоход км)
ответ. 192 км.
