Пусть х км/ч - новая скорость автобуса, тогда (х - 10) км/ч - прежняя скорость автобуса. Время движения сокращено на 1 час. Уравнение:
200/(х-10) - 200/х = 1
200 · х - 200 · (х - 10) = 1 · х · (х - 10)
200х - 200х + 2000 = х² - 10х
х² - 10х - 2000 = 0
D = b² - 4ac = (-10)² - 4 · 1 · (-2000) = 100 + 8000 = 8100
√D = √8100 = 90
х₁ = (10-90)/(2·1) = (-80)/2 = -40 (не подходит, так как < 0)
х₂ = (10+90)/(1·2) = 100/2 = 50
ответ: 50 км/ч.
Проверка:
200 : 50 = 4 ч - время движения по новому расписанию
200 : 40 = 5 ч - время движения по старому расписанию
5 ч - 4 ч = 1 ч - разница
1) Найдём производную: y' = 3x² + 18x + 15; Решим уравнение: 3x² + 18x + 15 = 0, x + 6x + 5 = 0, по теореме Виета: x₁ + x₂ = - 6, x₁ · x₂ = 5 ⇒
x₁ = - 1; x₂ =- 5 ⇒ на промежутке ( - ∞, - 5) функция возрастает;
на ( -5, - 1) убывает и на ( - 1, + ∞) возрастает, таким образом ( -5) - точка максимума, (-1) - точка минимума.
Вычислим: y (- 5) = (-5)³ + 9 · (-5)² + 15 · (-5) - 25 = 0; y (-1) = (-1)³ + 9 · (-1)² + 15 · (-1) - 25 = - 32
Итак: Строим график - От ( +∞) до точки ( - 5; 0) функция возрастает; От точки ( -5; 0) до точки (- 1; - 32) функция убывает и от точки ( -1; - 32)
до (-∞) возрастает.
Точки перегиба: ( -5; 0) и (- 1; - 32)
1)
а * (а+2) = 48
а**2 + 2а -48 = 0
а = -8 (нам не подходит) а = 6
ответ: 6 и 8
2)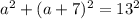
а = -12 (нам не подходит) а = 5
ответ: 5 и 12
3) (2а+1) * (2а+3) = 575
ответ 23 и 25
4)
а * (а-17) = 468
что-то в целых числах не получилось..