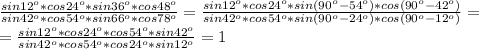
Объяснение:
0\hfill\\x-3>0\hfill\\x-3\ne1\hfill\\\end{gathered}\right.\Leftrightarrow\left\{\begin{gathered}x>-1\hfill\\x>3\hfill\\x\ne4\hfill\\\end{gathered}\right.\hfill\\\boxed{x\in(3;+\infty)}\hfill\\\end{gathered}\]" class="latex-formula" id="TexFormula2" src="https://tex.z-dn.net/?f=%5C%5B%5Cbegin%7Bgathered%7D2%29%5C%3B%5C%3B%7B%5Clog_%7Bx-3%7D%7D%28x%2B1%29%5Chfill%5C%5C%5Cleft%5C%7B%5Cbegin%7Bgathered%7Dx%2B1%3E0%5Chfill%5C%5Cx-3%3E0%5Chfill%5C%5Cx-3%5Cne1%5Chfill%5C%5C%5Cend%7Bgathered%7D%5Cright.%5CLeftrightarrow%5Cleft%5C%7B%5Cbegin%7Bgathered%7Dx%3E-1%5Chfill%5C%5Cx%3E3%5Chfill%5C%5Cx%5Cne4%5Chfill%5C%5C%5Cend%7Bgathered%7D%5Cright.%5Chfill%5C%5C%5Cboxed%7Bx%5Cin%283%3B%2B%5Cinfty%29%7D%5Chfill%5C%5C%5Cend%7Bgathered%7D%5C%5D" title="\[\begin{gathered}2)\;\;{\log_{x-3}}(x+1)\hfill\\\left\{\begin{gathered}x+1>0\hfill\\x-3>0\hfill\\x-3\ne1\hfill\\\end{gathered}\right.\Leftrightarrow\left\{\begin{gathered}x>-1\hfill\\x>3\hfill\\x\ne4\hfill\\\end{gathered}\right.\hfill\\\boxed{x\in(3;+\infty)}\hfill\\\end{gathered}\]">