
![\left(\dfrac{1}{4};\;\dfrac{1}{3}\right]](/tpl/images/1360/4170/bfd50.png)
Объяснение:
Рассмотрим сначала первое неравенство системы.
Начнем с ОДЗ:
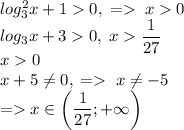
Продолжим решение:
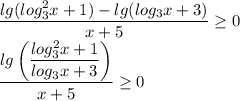
1)
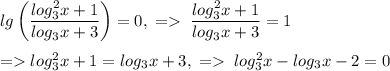
Замена: 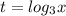 .
.
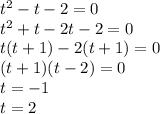
Обратная замена:
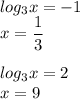
С учетом ОДЗ оба корня подходят.
2)
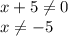
С учетом ОДЗ получим, что решение неравенства:
![x\in\left(\dfrac{1}{27};\;\dfrac{1}{3}\right]\cup[9;\;+\infty)](/tpl/images/1360/4170/0c6fd.png)
Теперь перейдем ко второму неравенству системы:
Понятно, что сначала нужно написать ОДЗ.
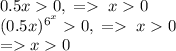
Продолжим решение:
![36^x+36\sqrt[4]{6}-6^{x+\frac{1}{4}}](/tpl/images/1360/4170/40301.png)
Заметим, что данное неравенство хорошо раскладывается на множители:
![36^x+36\sqrt[4]{6}-6^{x+\frac{1}{4}}](/tpl/images/1360/4170/de2d2.png)
Решим неравенство по методу интервалов.
1)
![\sqrt[4]{6}-6^x=0\\6^x=6^{\frac{1}{4}}\\x=\dfrac{1}{4}](/tpl/images/1360/4170/8f389.png)
2)
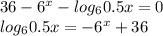
Введем функции 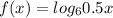 и
и 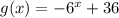 . Заметим, что первая функция возрастает, а вторая убывает. Поэтому, если уравнение имеет корень, он единственный. Теперь заметим, что x=2 - корень уравнения. Действительно,
. Заметим, что первая функция возрастает, а вторая убывает. Поэтому, если уравнение имеет корень, он единственный. Теперь заметим, что x=2 - корень уравнения. Действительно, 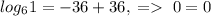 , верно. Так, мы решили это уравнение, получив, что его корень x=2.
, верно. Так, мы решили это уравнение, получив, что его корень x=2.
Тогда решение неравенства с учетом ОДЗ:
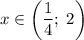
Итого имеем:
![x\in\left(\dfrac{1}{27};\;\dfrac{1}{3}\right]\cup[9;\;+\infty)\\x\in\left(\dfrac{1}{4};\;2\right)](/tpl/images/1360/4170/0ebfe.png)
Найдем пересечение:
![x\in\left(\dfrac{1}{4};\;\dfrac{1}{3}\right]](/tpl/images/1360/4170/792e3.png)
Задание выполнено!
1) Подставим корень в уравнение
Так как p и q - целые, а корень из трех вообще иррациональный, никаким домножением на целое число его не сделать целым. Если только не умножать на 0. Поэтому
p = -4
7+2p+q = 0
q = 1
2) Подставим корни p и q в это уравнение. Имеем
Либо q = 0 и p = 0
Либо p = -q-1 ≠ 0 и тогда
Второй вариант не подойдет, потому что у получающегося уравнения есть только один корень -1/2, но второй с ним не совпадает
3) Пусть меньший корень равен p, тогда больший - 2p.
Очевидно a = 0 не подходит, имеем после подстановки
Отметим что a не может равняться двум, потому что тогда 2p = p=0, а при a=2 корни уравнения 0 и 2.
Подставим этот корень в исходное уравнение
Почему надо пытаться вынести a=2? Потому что при a=2 формально p=2p, и значит у полученного кубического уравнения a=2 должно быть корнем. Но нас интересуют другие a
a = 3, x^2-3x+2, корни 1 и 2
a = 6, x^2-6x+8, корни 2 и 4
ответ: при a = 3 или 6