Объяснение:
Проблемы, указанные автором: проблемы демографии, безработица, неполное использование социальных и экономических возможностей общества, дефицит и нерациональное управление ресурсами, неэффективность принимаемых мер, инфляция, отсутствие безопасности и гонка вооружений, загрязнение среды и разрушение биосферы, заметное уже сегодня воздействие человека на климат.
Фрагмент текста: «нынешняя, полная чудес и противоречий фаза прогресса, принеся человеку множество щедрых подарков, в то же время глубоко изменила нашу маленькую человеческую вселенную, поставила перед человеком невиданные доселе задачи и грозит ему неслыханными бедами».
Примеры противоречивости прогресса:
1) развитие атомной электроэнергетики позволяет повысить эффективность производства, однако может быть опасным для окружающей среды и человека в случае аварий на АЭС;
2) использование Интернета позволяет увеличить темы коммуникации между людьми, при этом может вызвать определённую зависимость и другие психологические проблемы;
3) развитие биоинженерии и исследований в области генетики выводит на новый уровень возможности медицины по лечению и профилактике болезней, но при этом создаёт множество этических проблем (например, клонирование).
Мир стремительно меняется, особенно в области новых технологий, человек не успевает адаптироваться к новым возможностям, и это порождает ряд проблем (технологические аварии, структурная безработица и т. д.).
В условиях крайней нестабильности и неустойчивости человеку психологически трудно справляться с вызовами времени, и это, в свою очередь, усиливает трудность адаптации к новым изменениям.
Изменения культуры и общества происходят неравномерно: для разных регионов мира актуальны разные запросы, что делает затруднительным поиск ответов в вопросе решения глобальных проблем.
Откуда задание и тот ли это предмет?
Какой формулой пользоваться значения не имеет. На фотографиях представлены решения уравнения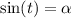
.
Если нарисовать числовую окружность, то значение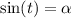
есть координата точки 
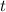по оси 
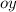, ведь для любой точки числовой окружности справедливо, что 
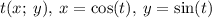, т.е. точка 
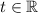имеет координаты 
.
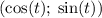Если провести прямую, параллельную оси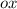
через точку 
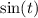, то она пересечётся с числовой окружностью в каких-то точках.
Чтобы было понятнее, советую нарисовать окружность радиусом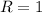
и центром в точке 
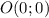и отмечать всё, о чём я пишу.
Теперь рассмотрим эти точки пересечения.
Если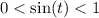
, то пересечения будут в первой и второй четвертях.
Если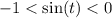
, то пересечения будут в третьей и четвёртой четвертях.
Если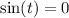
, то пересечений тоже два и это 
и 
.
Если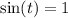
, то пересечение только одно, при чём точка пересечения будет и точкой касания, и равна она 
.
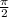Если же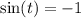
, то пересечение тоже одно, тоже является точкой касания, но значение равно 
.
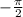А теперь вспомним определение арксинуса. Арксинусом числа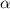
называют такой угол 
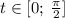, что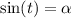 
. Главное здесь то, что 
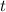может быть углом только первой четверти.
Отсюда же следует, что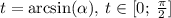
.
Это прекрасно работает для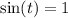
, ведь 
.
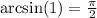Но только недавно мы проверили, что у нас может быть и не одно, а два решения. Как поступить в случае, если арксинус работает только для углов первой четверти, а нам нужно, чтобы он работал во второй? ответ прост.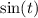
- это число, а 
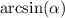- угол.
Пусть прямая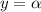
пересекается с окружностью в точках 
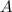в первой четверти и 
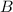во второй четверти, а точку 
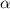на оси 
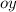мы обзовём 
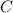. Рассмотрим треугольник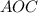и 
и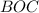 
, в них:
Треугольник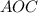и
и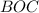 
равны по двум катетам. Из этого следует и то, что их соответственные углы равны. Т.е. угол 
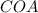и угол 
.
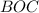Но углы мы отсчитываем от точки
, обзовём её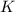 
. Тогда угол 
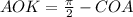. А это угол 
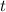первой четверти.
А угол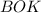
- искомый угол второй четверти.
Как нам известно, все числа на числовой окружности получаются с поворота на определённый угол, пусть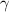
- этот угол. И если мы сделаем полный оборот, то мы хоть и придём в ту же самую точку, но вот число уже будет другое, ведь поворачивались мы на другой угол, равный 
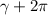. Таким образом, чтобы описать все числа, находящиеся в точке на окружности с координатами 
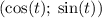надо добавить 
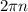, где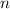 
- целое (чтобы получились полные обороты).
Вот так и получается первая формула.
Что до второй, то тут всё проще. Выводить её не буду, и так ответ уже километровый. В ней всё работает на чётности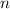
. Если 
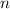- чётное, то формула трансформируется в 
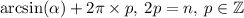, если нечётное, то в 
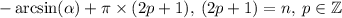, ну а 
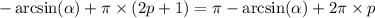. Т.е. это тоже самое, только записанное в одну строчку. Использовать вторую формулу не советую. Она менее интуитивно понятная. Но если в ней разобраться, то решение уменьшается в размере, это правда.
Как-то так. Фу-у-у-ух. Много. Очень Много Букв.
P.S. Прости за задержку.