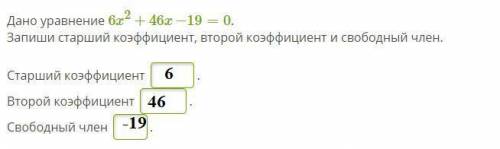
№1 (ответ на фото)
Квадратным уравнением называют уравнение вида ах²+bх+с=0, где коэффициенты а, b, с - любые действительные числа, причём, а≠0. Коэффициенты а, b, с, различают по названиям: а - первый или старший коэффициент; b - второй или коэффициент при х; с - свободный член, свободен от переменной х
№2 ( ответ на фото)
Приведенное квадратное уравнение – уравнение вида , первый коэффициент которого равен единице
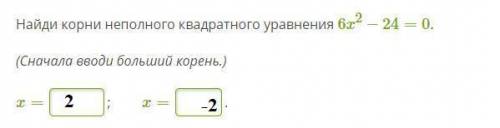
№3.
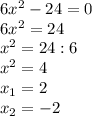
ответ: ±2
№4.
8x²+6x+9=0
a=8 b=6 c=9
D=b^2-4ac=6^2-4*8*9=36-288=-252
№5
x²+14x-8=0
D=14²-4*1*(-8)=196+32=228
√D=√228=2√57
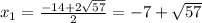
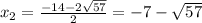


n 2x = 2 sinx * cos x
выносим из числителя 2 sinx. lim(x->0) 2 sinx/ х = 2
осталось вычислить lim(x->0) [cos x - 1 ] / ln cos(5x) неопределенность 0 на 0.
Проще всего по Лопиталю - вычислить производные числителя и знаменателя
Без Лопиталя
cos x -1 = - 2 sin^2 (x/2)
ln cos(5x) = ln [1+ ( cos 5x - 1) ] = ln [ 1- 2 sin^2 (5x/2) ]
---> - 2 sin^2 (5x/2)
после подстановки имеем
lim(x->0) { - 2 sin^2 (x/2) } / { - 2 sin^2 (5x/2) } = lim(x->0) { x^2/4 * [ sin^2 (x/2) / (x/2)^2} / { 25 x^2/4 * [sin^2 (5x/2)/(5x/2)^2 }=
= lim(x->0) { x^2 / 25 x^2 } =1/25
[ sin^2 (x/2) / (x/2)^2}=1 [sin^2 (5x/2)/(5x/2)^2 =1
m = -0,8
n = 0,2
Объяснение:
(m+1)x-ny=2n
mx+(n+1)y=5m
(-4;-6) ⇒ x = -4, y = -6, подставим в систему
-4(m+1) + 6n = 2n
-4m -6(n+1) = 5m
m+1 = n
6n+6= -9m
n = m+1 подставим во 2-е
2n+2 = -3m
2m+4 = -3m
n = m+1
5m = -4
n = m+1
m = -0,8
n = 0,2