
х - ширина прямоугольника
х + 8 - длина прямоугольника
(х + 8) * х = 65
х² + 8х - 65 = 0
Получили квадратное уравнение, ищем корни
х первое, второе = (-8 плюс минус √64+260) / 2
х первое, второе = (-8 плюс минус √324) / 2
х первое, второе = (-8 плюс минус 18) / 2
Отрицательный корень сразу отбрасываем, так как ширина не может быть отрицательной.
х = 5 это ширина прямоугольника (b)
5+ 8 = 13 это длина прямоугольника (а)
Р(периметр прямоугольника) = 2а + 2b
Подставляем, находим периметр
Р = 2 * 13 + 2 * 5 = 36 (см)
Пояснение:
(!) Одно из свойств уравнений: любое число в уравнении можно перенести через знак равно (т. е. из левой части уравнения в правую, или из правой части в левую. При этом (обычно) переменные переносятся в левую часть уравнения, а числа - в правую) изменив знак перед числом на противоположный ("+" на "-" ; "-" на "+"). Такое уравнение будет равносильно исходному уравнению.
(!) При упрощении выражения и решения уравнения воспользуемся распределительным свойством умножении, относительно действия сложения и вычитания:
a × (b + c) = ab + ac.
a × (b - c) = ab - ac.
1) x (x - 8) - 20 = - 15 - x (1 - x);
x² - 8x - 20 = - 15 - x + x²;
x² - x² - 8x + x = - 15 + 20;
- 7x = 5;
x = 5 ÷ (- 7);
x = - .
.
__________
ответ: - .
.
2) 47 - x (11 - x) = 19x + x²;
47 - 11x + x² = 19x + x²;
x² - x² - 11x - 19x = - 47;
- 30x = - 47;
x = - 47 ÷ (- 30);
x =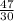 ;
;
x =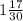
__________
ответ: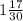 .
.
3) 33x - x² = (35 - x) x - 17;
33x - x² = 35x - x² - 17;
- x² + x² + 33x - 35x = - 17;
- 2x = - 17;
x = - 17 ÷ (- 2);
x = 8,5.
__________
ответ: 8,5.
4) 59x + 4x² = - 4x (1 - x) + 21
59x + 4x² = - 4x + 4x² + 21
4x² - 4x² + 59x + 4x = 21
63x = 21
x = 21 ÷ 63
x =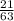
x =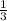 .
.
__________
ответ: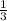 .
.
__________________
Удачи! :)