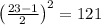Решите задание на производную с объяснением каждого шага. На рисунке изображён график функции y=f(x) . На оси абсцисс отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Замечаем, что перестановки происходят отдельно среди четных чисел и среди нечетных чисел. Поэтому надо ответить на следующий вопрос: есть k предметов, расставленных в каком-то порядке слева-направо и соответствующим образом занумерованных; меняя местами за одну операцию два соседних предмета, нужно расставить их в том же порядке, но справа-налево. Говоря ученым языком, можно сказать, что сначала у нас не было ни одной инверсии (инверсия - это когда предмет с меньшим номером стоит правее предмета с большим номером), а надо сделать максимальное количество инверсий. Меняя местами соседей, мы каждый раз изменяем количество инверсий на 1. Конечно, нам невыгодно уменьшать количество инверсий, а выгодно - увеличивать. Но в каком порядке производить эту операцию - менять местами соседей - абсолютно непринципиально. Поступим, скажем, так. Поменяем сначала местами первый предмет и второй, затем первый и третий, первый и четвертый, и так далее, наконец, первый и последний. Всё. Первый предмет оказался на нужном месте и больше оттуда никуда сдвигаться не будет. Потребовалось нам для этого, естественно, (k-1) операция. Далее будем передвигать второй предмет до тех пор, пока он не поменяется местами с k-м предметом и не окажется рядом с первым, но левее первого. На это потребуется (k-2) операции. И так далее. Всего мы насчитаем операций.
Остается подвести итоги. Окончательный ответ зависит от того, каково n - четное оно или нечетное.
1-й случай: n - четное, n=2m. Это означает, что у нас m четных чисел и m нечетных чисел. Всего операций получится
2-й случай. n - нечетное, n=2m+1. Это означает, что у нас m четных чисел и (m+1) нечетных чисел.Всего операций получится
КЛАССИФИКАЦИЯ: Линейное неоднородное дифференциальное уравнение второго порядка со специальной право частью Найти нужно: yо.н. = уо.о. + уч.н.
Найдем уо.о. (общее однородное) Применим метод Эйлера Пусть , тогда подставив в однородное уравнение, получаем характеристическое уравнение Корни которого Тогда общее решение однородного уравнения будет
Найдем теперь уч.н.(частное неоднородное) отсюда где - многочлен степени х
Сравнивая с корнями характеристического уравнения и, принимая во внимания что n=1 , частное решение будем искать в виде: уч.н. =
Чтобы определить коэффициенты А и В, воспользуемся методом неопределённых коэффициентов:
Подставим в исходное уравнение и приравниваем коэффициенты при одинаковых х
Тогда частное решение неоднородного будет иметь вид
Замечаем, что перестановки происходят отдельно среди четных чисел и среди нечетных чисел. Поэтому надо ответить на следующий вопрос: есть k предметов, расставленных в каком-то порядке слева-направо и соответствующим образом занумерованных; меняя местами за одну операцию два соседних предмета, нужно расставить их в том же порядке, но справа-налево. Говоря ученым языком, можно сказать, что сначала у нас не было ни одной инверсии (инверсия - это когда предмет с меньшим номером стоит правее предмета с большим номером), а надо сделать максимальное количество инверсий. Меняя местами соседей, мы каждый раз изменяем количество инверсий на 1. Конечно, нам невыгодно уменьшать количество инверсий, а выгодно - увеличивать. Но в каком порядке производить эту операцию - менять местами соседей - абсолютно непринципиально. Поступим, скажем, так. Поменяем сначала местами первый предмет и второй, затем первый и третий, первый и четвертый, и так далее, наконец, первый и последний. Всё. Первый предмет оказался на нужном месте и больше оттуда никуда сдвигаться не будет. Потребовалось нам для этого, естественно, (k-1) операция. Далее будем передвигать второй предмет до тех пор, пока он не поменяется местами с k-м предметом и не окажется рядом с первым, но левее первого. На это потребуется (k-2) операции. И так далее. Всего мы насчитаем операций.
операций.
Остается подвести итоги. Окончательный ответ зависит от того, каково n - четное оно или нечетное.
1-й случай: n - четное, n=2m. Это означает, что у нас m четных чисел и m нечетных чисел. Всего операций получится
2-й случай. n - нечетное, n=2m+1. Это означает, что у нас m четных чисел и (m+1) нечетных чисел.Всего операций получится
Решим задачу для n=5, 6, 7, 23.
n=5 - нечетное;
n=6 - четное;
n=7 - нечетное;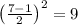
n=23 - нечетное;