Сначала нужно найти производную. Она будет равна (e^x)+x*(e^x)
Найдем критические точки функции (это точки, в которых функция не существует или равна нулю):
(e^x)+x*(e^x)=0
e^x(1+x)=0
e^x=0 решений нет
1+х=0
х=-1
Т.е. возможен экстремум в точке х=-1.
Теперь нужно узнать знак производной слева и справа от х=-1 (сначала берешь любую точку из промежутка (-беск.;-1) и вычисляешь значение производной, затем любую точку из промежутка (-1;+беск.) и также вычисляешь значние производной).
Значение производной на первом промежутке отрицательно, следовательно, на нем функция убывает, на втором промежутке значение производной положительно, следовательно, на нем функция возрастает.
Производная меняет знак с минуса на плюс, следовательно, х=-1 минимум функции.
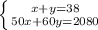
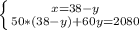
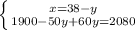
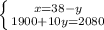
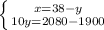

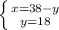
(2,6 x 0,3 - 2 4/15 : 5 2/3) : (-1,9)
1) 2,6 x 0,3= 0,78
2) 2 4/15 : 5 2/3 = 34/15: 17/3= 34/15 x 3/17= 2/5= 0,4 ( сокращаем 34 и 17, а именно 34: 17=2 ; сокращаем 15 и 3, а именно 15:3=5; после 2/5 переводим в десят. дробь и получаем 0,4)
3) 0,78 - 0,4= 0,38
4) 0,38 : (-1,9)= - 0,2