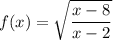
Подкоренное выражение должно быть неотрицательным, а знаменатель не равен нулю. При записи первого условия, второе учитывается. Тогда имеем:
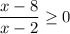
Решим методом интервалов:
Отмечаем на координатной прямой точки, в которых выражения из знаменателя и числителя обращаются в ноль. И выкалываем 2 т.к. на ноль делить нельзя. Мы получили 3 интервала. Перед дробью знак положителен, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (нету чётных степеней, где знак может не измениться). Нас интересует, когда больше или равно, поэтому выбираем интервалы с плюсом, учитывая их границы.
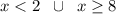
ответ: x∈(-∞;2)∪[8;+∞).

Нужно чтобы при сложении получилось уравнение с одной неизвестной.
Ее найти и подставив в любое уравнение из системы - найти вторую неизвестную.
Например:
2х+у=4
х-2у=7
Умножим почленно первое уравнение на 2: 4х+2у=8
сложим со вторым: 4х+х-2у+2у=8+7
Отсюда 5х=15
х=3
у=4-2х=-2 ( из первого уравнения)
Чтобы посторить график системы берешь любые значения х и у и подставляешь их в оба уравнения.
Например х=0 у=4-2х=4 Первая точка с координатами (0;4) -для первой прямой.
Теперь во второе - х=0, у=(х-7)/2 =-3,5 Первая точка с координатами (0;-3,5) - для второй прямой.
Потом берешь х=1 и так далее. По полученым точкам строишь прямые.
Точка их пересечния и есть решение системы уравнений.