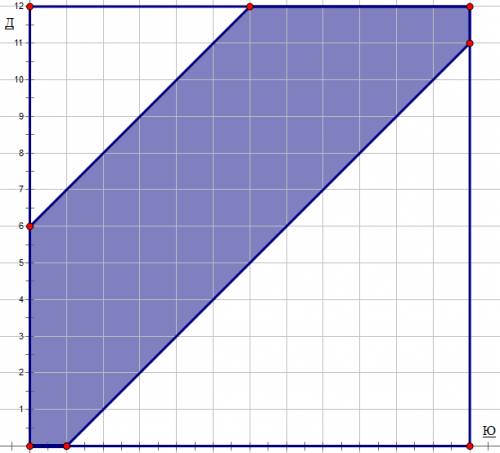
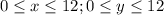 . Теперь найдем, каким точкам соответствует событие "встреча состоялась". Дополнительно ко всему нижеследующему налагается условие, что точки вне квадрата не рассматриваются.
. Теперь найдем, каким точкам соответствует событие "встреча состоялась". Дополнительно ко всему нижеследующему налагается условие, что точки вне квадрата не рассматриваются.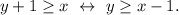 . Заметим, что условие также выполняется, если юноша приходит первым, т.к. тогда правая часть отрицательна.
. Заметим, что условие также выполняется, если юноша приходит первым, т.к. тогда правая часть отрицательна.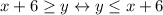 .
.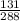 .
. 
v первого велосипедиста x км/ч, v второго x-5 км/ч.
Тогда первый за 1 час 20 минут путь (18+S) км:
(18+S) / x = 4/3
Х = 3 * (18+S) / 4
Второй велосипедист путь 18-S км за 1ч 20 мин
(18-S) / (х-5) = 4/3
(18+S) / x = (18-S) / (х-5)
(18+S) (x-5) = (18-S) x
18x - 90 + Sx - 5S = 18x - Sx
2Sx - 5S - 90 = 0
S (Х = 3 * (18+S) / 4)
2S * 3 (18+S) / 4 - 5S - 90 = 0
1.5 S (18+S) - 5S - 90 = 0
1.5 S^2 + 27S - 5S - 90 = 0
1.5S^2 + 22S - 90 = 0
D = 22^2 + 4*1.5 * 90 = 484 + 540 = 1024 = 32^2
S1 = (-22 - 32)/3 <0 - не подходит
S2 = (-22+32)/3 = 10/3 = 3 1/3
ответ: 3 1/3 км