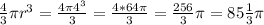Хорошо, я с удовольствием помогу вам разобраться с этим математическим вопросом.
Для начала, давайте найдем корни уравнения x²-7x+6=0.
Мы можем найти корни этого квадратного уравнения, используя метод разложения на множители или используя формулу корней. Воспользуемся формулой корней, так как она может быть полезна в других случаях также.
Формула корней квадратного уравнения x²+bx+c=0 выглядит следующим образом:
x = (-b ± √(b²-4ac))/(2a)
В нашем уравнении x²-7x+6=0, a=1, b=-7 и c=6.
Теперь, пошагово, вычислим корни:
Делаем подстановку в формулу корней:
x = (-(-7) ± √((-7)²-4(1)(6)))/(2(1))
Теперь, найдем корни уравнения x³-x=0. Мы видим, что это кубическое уравнение.
Однако, в данном вопросе, у нас есть особенность - символ i. i - это мнимая единица, которая представляет собой квадратный корень из -1. Для решения этого уравнения, нам нужно использовать комплексные числа.
Уравнение x³-x=0 можно факторизовать, вынеся x за скобки:
x(x²-1)=0
В этом случае, у нас есть два возможных корня - x=0 и x²-1=0. Давайте решим это уравнение для второго корня.
x²-1=0
x²=1
Это квадратное уравнение, в котором a=1, b=0 и c=-1.
Используем формулу корней, чтобы найти корни:
x = (-0 ± √(0²-4(1)(-1)))/(2(1))
x = (±√(0+4))/(2)
x = (±√(4))/(2)
x = (±2)/(2)
Мы получили два возможных корня: x₁=1 и x₂=-1.
Теперь у нас есть ответы на оба уравнения:
Корни уравнения x²-7x+6=0 равны 6 и 1.
Корни уравнения x³-x=0 равны 0, 1 и -1.
Теперь давайте сравним меньший корень из первого уравнения (x=1) с большим корнем из второго уравнения (x=1).
Меньший корень у первого уравнения равен 1, а больший корень у второго уравнения также равен 1.
Итак, мы можем сделать вывод, что меньший корень уравнения x²-7x+6=0 совпадает с большим корнем уравнения x³-x=0.
Чтобы представить вектор AB в виде линейной комбинации векторов AC, BE, EC, CB и BA, мы можем использовать принцип векторной алгебры, согласно которому вектор может быть представлен как сумма или разность других векторов.
Давайте рассмотрим каждый из векторов, используемых в линейной комбинации:
1. Вектор AC: Это вектор, который идет от точки A до точки C. Мы можем представить его просто как сам вектор AC.
2. Вектор BE: Это вектор, который идет от точки B до точки E. Как мы можем представить его через векторы AC и CB? Мы знаем, что вектор CB указывает от точки C до точки B, поэтому мы можем использовать его как отрицательный вектор, а затем сложить с вектором AC. Таким образом, вектор BE можно представить как BE = AC + (-CB).
3. Вектор EC: Это вектор, который идет от точки E до точки C. Мы можем представить его как противоположный вектор вектору CE. Мы уже знаем, что вектор CE равен AC - EC, поэтому мы можем просто изменить его направление: EC = -(AC - EC) = -AC + EC.
4. Вектор CB: Мы уже использовали его в предыдущем пункте для представления вектора BE. Вектор CB может быть представлен как сам CB.
5. Вектор BA: Это вектор, который идет от точки B до точки A. Как мы можем представить его через векторы AC и CB? Мы знаем, что вектор AC указывает от точки A до точки C, поэтому мы можем использовать его как отрицательный вектор, и затем сложить его с вектором CB. Таким образом, вектор BA можно представить как BA = -AC + CB.
Таким образом, мы можем представить вектор AB как линейную комбинацию векторов: AB = AC + (-CB) + (-AC + EC) + CB + (-AC + CB).
Для школьного ученика, которому нужно понять эту концепцию, мы можем привести пример, чтобы это стало более понятным. Допустим, у нас есть школьный коридор с пятью комнатами (A, B, C, D, E), и вектор AB представляет путь от комнаты A до комнаты B.
- Вектор AC может быть выражен просто как проход через комнаты A и C.
- Вектор BE может быть выражен как путь через комнаты B, C и E (AC + (-CB)).
- Вектор EC может быть выражен как путь через комнаты E, C и A (-AC + EC).
- Вектор CB является путем от комнаты C до комнаты B.
- Вектор BA может быть выражен как путь через комнаты B, C и A (-AC + CB).
Таким образом, вектор AB может быть представлен как сумма этих путей: AB = AC + (-CB) + (-AC + EC) + CB + (-AC + CB).
Я надеюсь, что это объяснение помогло и стало понятным!
Площадь поверхности шара - 64π
Формула площади -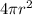
Получаем уравнение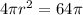 ⇒
⇒ 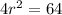 ⇒
⇒ 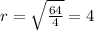
Объем шара: