Если я правильно понял задание то:
Составим векторы c1 и c2 для этого вместо а и b подставим значения координат векторов приведенных в задании и руководствуясь правилами умножения и сложения векторов получим
![c1=2*\left[\begin{array}{c}-9\\5\\3\end{array}\right]-\left[\begin{array}{c}7\\1\\-2\end{array}\right] c2 = 3* \left[\begin{array}{c}-9\\5\\3\end{array}\right]+5*\left[\begin{array}{c}7\\1\\-2\end{array}\right]](/tpl/images/0065/4758/31ddd.png)
Получаем Необходимым и достаточным условие коллинеарности двух векторов является равенство нулю их векторного произведения
векторное произведение [a,b] для произвольных векторов а=(а1,а2,а3) и b=(b1,b2,b3) вычисляется по формуле
[a,b]={a2*b3-a3*b2; a3*b1-a1*b3; a1*b2-b1*a2}
Вычисляя по этой формуле векторное произведение c1 и с2 получаем:
[c1,c2]={-169; 39; -572} он не равен нулевому вектору, значит вектора не коллинеарны Векторы будут коллинеарны тогда и только тогда, когда существует такая константа m, что с1=m*c2
чтобы выяснить ее существование рассмотрим соотношение соответсвующих координат векторов c1 и с2
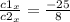
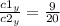
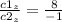
Получаем что:
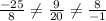
Значит такой константы m не существуют, векторы не коллинеарны
,
, a 
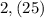
целая часть. У нас она равна 2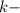
- количество цифр в периоде. У нас их 2
количество цифр до периода. У нас их 0
все цифры, включая период, в виде натурального числа. У нас это 25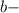
все цифры без периода в виде натурального числа. Их нет.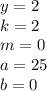
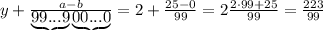
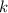подставляется количество 9, а под 
-количество нулей. У нас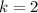 
, значит пишем две цифры 9, а 
, значит, нулей не пишем вообще. Между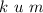 
не стоит знак умножения
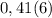
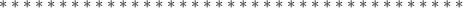
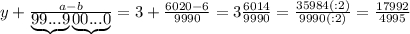
x^2+7xy+3y^2-x^4-6x^2y^2-9y^4
Объяснение: