Условие. Y²+xy-4x-9y+20=0 ; y=ax+1 ; x>2
найти все значения а, при которых графики имеют одну общую точку(в нашем случае (ax+1)² + x(ax+1) -4x - 9(ax+1)+20=0 имеет единственное решение).
Подставим у = (ax+1)² в уравнение у²+xy-4x-9y+20=0, получим
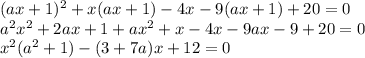
Найдем дискриминант квадратного уравнения относительно x
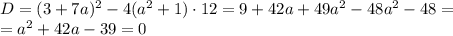
Получим 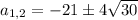
Если подставить 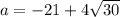 , т.е. имеется квадратное уравнение
, т.е. имеется квадратное уравнение  , у которого корень
, у которого корень
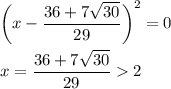
Если подставить  , т.е. имеется квадратное уравнение
, т.е. имеется квадратное уравнение 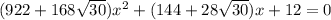 , у которого корень
, у которого корень
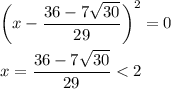
ответ: 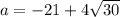
2, 4,5, 10, 3,2, 14, 2, 48, 0,5...
Объяснение:
1) а) 1/2*16+1,5*0,8=8+1,2=2
б) 6,5-3*2/3=6,5-2=4,5
в) 4*2,5=10
2) а) √10,24=3,2
б) √(7*28)=√196=14
в) √(32/8)=√4=2
г) 4^2×3=16*3=48
3) a) x=0.5, x=-0.5
б) х=√15, х=-√15
в) x²=-3+3 x²=0 х=0
г) решений нет. число в квадрате не может быть отрицательным