Відповідь:Если все одёмные, то 0, а если 69 натуральное (+69), то 69
Пояснення:
x принадлежит (-бесконечности; 2-2*2^(1/2)] U {2} U [2+2*2^(1/2); + бесконечность)
Объяснение:
(x^2-4*x)^2 - 16 >=0
(x^2 - 4*x)^2 - 4^2 >=0
(x^2-4*x - 4)*(x^2 - 4*x + 4)>=0
(x^2 - 4*x - 4) * (x - 2) ^ 2 >= 0
найдем корни x^2 - 4*x - 4 = 0
D = 16 + 16 = 32
x = (4 - 4*2^(1/2))/2
x = (4 + 4*2^(1/2))/2
2^(1/2) - корень из двух
нули функции
+++ --- +
2 - 2*2^(1/2) 2(корень четной степени) 2 + 2*2^(1/2)
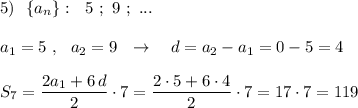

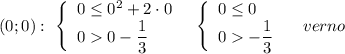
Для других точек хотя бы одно неравенство будет неверным.
Например,
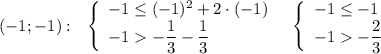 неверно 2 неравенство
неверно 2 неравенство
7) Из города А в город В ведут 8 дорог. Обозначим их: 1,2,3,4,5,6,7,8 .
Из города В в город С ведут 9 дорог. Обозначим их: a,b,c,d,e,f,g,i,k .
Тогда можно написать, какие маршруты могут быть.
(1,a) (1,b) (1,c) (1,d) (1,e) (1,f) (1,g) (1,i) (1,k)
(2,a) (2,b) .......................................................... (2,k)
(3,a) (3,b)............................................................. (3,k)
........................................................................................
(8,a) (8,b).............................................................. (8,k)
Образовалась таблица из 8 строчек и 9 столбцов. Количество элементов в этой таблице равно 8*9=72 . Поэтому и маршрутов может быть 72 .
-2/5
Объяснение:
потому что оно лежит на числ.прямой правее чем остальные числа