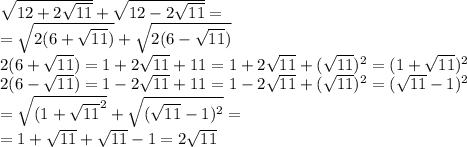
Чтобы выяснить,какая из точек не принадлежит графику достаточно координаты этих точек подставить в функцию,которой задан график.
Если получится верное равенство,то точка принадлежит графику, а если неверное, то не принадлежит.
Данная функция прямая, параллельная оси ОХ, вида
у=k*х+b
k=0
k – угловой коэффициент , b – свободный член(-5) , x – независимая переменная.
у=0*х-5
НО
Мы видим , что данная функция не зависит от Х, при любом его значении у=-5 , то есть можно без расчетов найти точку,которая не принадлежит графику. Это точка 3, потому что у=0,а не -5.
Если мы этого не видим,то подставляем:
1) (0: -5)
-5=0*0-5
-5=-5 - принадлежит
2) (-5:-5)
-5=0*-5-5
-5=-5 - принадлежит
3) (-5: 0 )
0=0*-5-5
0≠-5 - не принадлежит
4) (5: -5 )
-5=0*5-5
-5=-5 - принадлежит
Объяснение:
sin1845° можно представить как sin(1800°+45°)
Так как π=180°, то 1800°=10π, то есть sin(1800°+45°)=sin(10π+45°)
Дальше есть несколько путей нахождения необходимого значения. Во-первых, период синуса - 2π, то есть sin(2π+x)=sin(x), тогда sin(10π+45°)=sin(45°)=√2/2
Во-вторых, можно раскрыть по формуле синуса суммы:
sin(a+b)=sin(a)cos(b)+cos(a)sin(b)
sin(10π+45°)=sin(10π)cos(45°)+cos(10π)sin(45°)=0*√2/2+1*√2/2=√2/2
В-третьих, можно узнать значение функции с формул приведения. Так как аргумент отсчитывается от горизонтальной оси, смены функции на кофункцию (косинус) не будет; изначальная функция положительна (I четверть на тригонометрической окружности), поэтому знак будет тоже "+".
√(12+2√11) + √(12-2√11) =√(1+11+2√11) + √(1+11-2√11)=√(1+√11)² + √(1-√11)²=
=|1+√11| + |1-√11| = (1+√11 )+( √11-1)=2√11
Так как 1-√11<0, то модуль |1-√11|=-(1-√11)=√11-1