
41-32х≥0;
9-3х≥0
5+х≥0
ОДЗ: х ∈[-5; 41/32]
Перепишем уравнение в виде
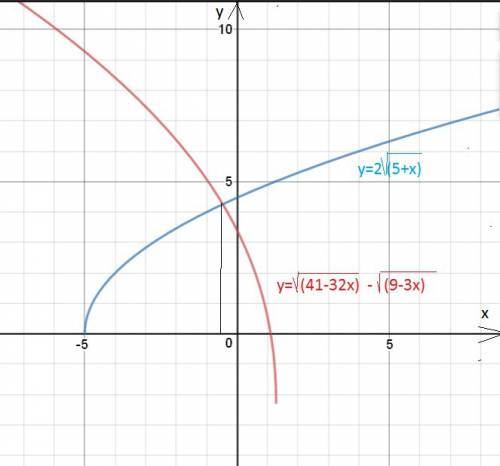
√(41-32x)=2√(5+x)+√(9-3x)
Возводим в квадрат.
41-32х=4(5+х)+4√(5+х)·√(9-3х)+9-3х
4√(5+х)·√(9-3х)=12-33х
Возводим в квадрат при условии 12-33х≥0 ⇒ х ≤12/33.
16(5+х)(9-3х)=144-792х+1089х²;
1137х²-696х-576=0
379х²-232х-192=0
D=(-232)²-4·379·(-192)=53 824+291 072=344 896
x=(232-√344896)/758≈-0,47 или х=(232+√344896)/758≈1,08 - не удовлетворяет условию х ≤12/33, поэтому не является корнем уравнения
ответ:
объяснение:
1) не верно, т.к. - не относится к множеству вещественных чисел.
2) не верно, т.к. -0.20 не относится к множеству вещественных чисел
3) верно, т.к. 0.2 можно представить в виде простой дроби 2/10 и оно является рациональным числом
4) верно, т.к. дробь -1/7 - простая, следовательно, оно относиться к множеству рациональных чисел
5) не верно, т.к. - - иррациональное число
6) верно, т.к. 7 - вещественное число
7) не верно, т.к. - иррациональное число
Сумма катетов прямоугольного треугольника равна 31 см,
а его гипотенуза равна 25 см. Найди площадь треугольника.
Обозначили длину одного катета как x см, а другого — y см.
Тогда x+y=31 — сумма катетов прямоугольного треугольника.
Применим теорему Пифагора:
x2+y2=252;x2+y2=625.
Получаем систему двух уравнений с двумя неизвестными:
{x+y=31x2+y2=625
Объяснение: