Question

3в степени (-0,5+х) умножить на 3 в степени (х-1)= 1 найти промежуток, которому принадлежит корень уравнения: 1) [-4; -2] 2) (-2; -1) 3) [-1; 0] 4) (1; 2)

Answer 1

3^(-0,5+х) * 3^(х-1) = 1

3^(2x-1,5) =1

2x - 1,5 = 0

x = 0,75 

Answer 2

$3^{-0,5+x}*3^{x-1}=1$

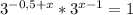
Воспользуемся свойствомстепени: если основания одинаковые, то показатели складываем, а основание оставляем прежним

$3^{-0,5+x+x-1}=1$

$3^{2x-1,5}=1$

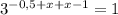
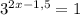
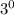
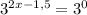
Представим 1 в виде $3^{0}$

$3^{2x-1,5}=3^{0}$

Т.к. основания равны, то и показатели будут равны, т.е.

$2x-1,5=0$

$2x=1,5$

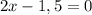
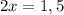
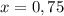$x=0,75$ или $x=\frac{3}{4}$

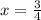
Среди вариантов ответа ни один промежуток не содержит данный корень, однако уравнение решено верно! Скорей всего ошибка в ответах, к сожалению, это не редкость.