
Основание пирамиды - прямоугольник со сторонами 6 см и 8 см.
Каждое боковое ребро пирамиды равно 13 см.
Вычислить высоту пирамиды.
Если все боковые ребра пирамиды равны между собой, то вершина пирамиды проецируется в центр описанной около основания окружности.
Диаметр окружности, описанной около прямоугольника, равен его диагонали.
Радиусы описанной окружности - проекция боковых ребер.
Диагональ прямоугольника - диаметр описанной окружности - найдем по т. Пифагора:
D=√(6²+8²)=10 см
R=5 cм
Высоту Н пирамиды найдем по т.Пифагора из прямоугольного треугольника, образованного
боковым ребром - гипотенуза,
высотой и радиусом описанной окружности - катеты. ( Можно без вычисления сказать, что она будет равна 12 - треугольник из Пифагоровых троек 5:12:13)
Н=√(13²-5²)=12 см
Основание пирамиды - прямоугольник со сторонами 6 см и 8 см.
Каждое боковое ребро пирамиды равно 13 см.
Вычислить высоту пирамиды.
Если все боковые ребра пирамиды равны между собой, то вершина пирамиды проецируется в центр описанной около основания окружности.
Диаметр окружности, описанной около прямоугольника, равен его диагонали.
Радиусы описанной окружности - проекция боковых ребер.
Диагональ прямоугольника - диаметр описанной окружности - найдем по т. Пифагора:
D=√(6²+8²)=10 см
R=5 cм
Высоту Н пирамиды найдем по т.Пифагора из прямоугольного треугольника, образованного
боковым ребром - гипотенуза,
высотой и радиусом описанной окружности - катеты. ( Можно без вычисления сказать, что она будет равна 12 - треугольник из Пифагоровых троек 5:12:13)
Н=√(13²-5²)=12 см
Объяснение:
(x-1)/4)-(2x-3)/2<(x²+3x)/8 - умножим на 8
2(x-1)-4(2x-3)<x²+3x
2х-2-8х+12<x²+3x
-6х+10<x²+3x
x²+3x>-6х+10
x²+9x-10>0
(x-1)(x+10)>0⇒ 1)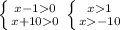 Отсюда (больше большего) х>1
Отсюда (больше большего) х>1
т.е х∈(1;+∞) либо
2)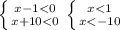 Отсюда(меньше меньшего) x<10 т.е.х∈(-∞;-10)
Отсюда(меньше меньшего) x<10 т.е.х∈(-∞;-10)
ответ: х∈(-∞;-10)∪(1;+∞)